【文献学习】热电偶信号调理电路、IOT接入和处理算法

2021.10 ~ 12 参与了一个高温高精度测温项目，任务是做一个高精度高温传感器配套测试系统。在此记录一些文献的学习笔记与参考。仅做记录总结，转载注明出处。

热电偶信号调理、IOT接入

1.基础知识复习

热电偶传感器利用热电效应来进行工作的, 其热电势率一般为几十到几μV/0℃。它直接和被测对象接触, 不受中间介质的影响, 因而测量精度高, 并且可以在-200 ~ 1600℃范围内进行连续测量。

理论上，热电偶是冷端以0℃(或者0K，看E（T，0）计算式的单位)为标准进行测量的。然而，通常测量时仪表是处于室温之下的，但由于冷端不为0℃，造成了热电势差减小，使测量不准，出现误差。因此为减少误差所做的补偿措施就是冷端温度补偿。

通常会采用一些措施来消除冷端温度变化所产生的影响，如冷端恒温法、冷端温度校正法、补偿导线法、补偿电桥法。

• （1）冷端恒温法

冷端恒温法就不说了，把冷端泡在冰水混合物里，不经济，难实现。

• （2）冷端温度校正法

由于热电偶的温度分度表是在冷端温度保持在0℃的情况下得到的，与它配套使用的测量电路或显示仪表又是根据这一关系曲线进行刻度的，因此冷端温度不等于0℃时，就需对仪表指示值加以修正。如冷端温度高于0℃，但恒定于t0℃,则测得的热电势要小于该热电偶的分度值，为求得真实温度，可利用中间温度法则，即用下式进行修正：

E（t,0）= E（t,t1）+ E（t1,0）

这里用到了一个热电偶重要的定律：中间温度定理，定义内容就是上面的式子。

3）补偿导线法

由于热电偶的材料一般都比较贵 (特别是采用贵金属时)，而测温点到仪表的距离都很远，为了节省热电偶材料，降低成本，通常采用补偿导线（compensating lead）把热电偶的冷端 (自由端)延伸到温度比较稳定的控制室内，连接到仪表端子上。这是一种专用导线，有正、负极性。选择某一对导线，当其与某种热电偶的热电特性小于100℃的范围里一致时，只要热电偶冷端小于100℃，并将它与热电偶冷端连结，则相当于将热电偶延长，这样便于热电偶的冷端温度处理，如果所移的冷端仍处于温度较高或有波动的地方，则此时的补偿导线就失去使用意义。

电桥补偿法其实就是冷端温度矫正的一种方法， 除此之外还有通过其他方式矫正的，这个会在下篇文献学习中详细描述。

2、基础信号调理电路

首先想到的就是某门课讲过的一种调理电路：

总结一下：偏置、滤波、放大。

这里冷端补偿的方式是外接温度传感器AD590，在AD转换输入单片机，软件部分进行冷端补偿。

书上就一电路图，没有分析过程，所以参数设计过程遇到了困难。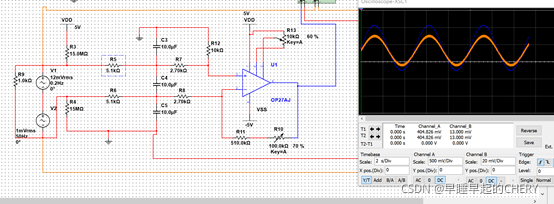

在调试仿真后发现，更改上拉电阻R1，可以改变偏置，如果上拉电阻小是反偏，电阻大是正偏置。上拉电阻一般要比后面的滤波器电阻大几个量级；上拉电阻过小会导致反偏的厉害，在输出后级再加反相器也能起到调偏置的目的，但是多个有源器件引入噪声。 选择上拉电阻大三个量级，滤波器电阻5.1k，正向偏置400mV左右，在输入信号为正时可以保证正偏；在输入信号为0时输出恒定偏置值，再通过运放offset调整。
原电路加偏置是为了适应运放单电源供电的工作状态，在仿真后偏置效果不太能保证，所示在PCB中加了分压电路，为运放双端供电，分压中间点位模拟地，接入板子公共地。

调整R5对输出幅值改变明显；信号截止频率通过调整电容来改变。分压电阻后面的无源滤波器，滤波截止频率主要又电容确定，大电容滤低频，图示值能滤除工频干扰。

调整OP系列运放的OFFSET端电压能有效改善零输入失调电压，调整范围在100mA左右。

3、其他相关信号调理

在买的读数头（温度配送器）中，大多有一个转4-20mA输出的功能，之前也有很多传感器调理电路需要这类输出，但没深究为什么。在百度查了一些相关文章，电子发烧友一篇文章写的很好：

采用电流信号的原因是不容易受干扰，因为工业现场的噪声电压的幅度可能达到数V，但是噪声的功率很弱，所以噪声电流通常小于nA级别，因此给4－20mA传输带来的误差非常小；电流源内阻趋于无穷大，导线电阻串联在回路中不影响精度，因此在普通双绞线上可以传输数百米；由于电流源的大内阻和恒流输出，在接收端我们只需放置一个250欧姆到地的电阻就可以获得0－5V的电压，低输入阻抗的接收器的好处是nA级的输入电流噪声只产生非常微弱的电压噪声
上限取20mA是因为防爆的要求：20mA的电流通断引起的火花能量不足以引燃瓦斯。下限没有取0mA的原因是为了能检测断线：正常工作时不会低于4mA，当传输线因故障断路，环路电流降为0。常取2mA作为断线报警值。电流型变送器将物理量转换成4 - 20mA电流输出，必然要有外电源为其供电。最典型的是变送器需要两根电源线，加上两根电流输出线，总共要接4根线，称之为四线制变送器。当然，电流输出可以与电源公用一根线（公用VCC或者GND），可节省一根线，所以现在基本上将四线制变送器称之为三线制变送器。其实大家可能注意到， 4-20mA电流本身就可以为变送器供电，变送器在电路中相当于一个特殊的负载，这种变送器只需外接2根线，因而被称为两线制变送器。
4-20mA.DC（1-5V.DC）信号制是国际电工委员会（IEC）：过程控制系统用模拟信号标准。我国从DDZ-Ⅲ型电动仪表开始采用这一国际标准信号制，仪表传输信号采用4 ~ 20mA.DC，联络信号采用1 ~ 5V.DC，即采用电流传输、电压接收的信号系统。

所以在第一版电路板上加入了V-A转换与A-V转换，以适应长距离传输情况，具体转换电路百度随便查一下，有很多。

4、软件设计基础

设计配套测试系统，重点部分在数据处理方式，这部分在下篇讲解。在此记录几篇有关信号安全传输、IOT系统接入和UI界面设计的文章：

[1]Chang, V., Martin, C., 2021. An industrial IoT sensor system for high-temperature measurement. Computers & Electrical Engineering 95, 107439.. doi:10.1016/j.compeleceng.2021.107439

[2]T. Xu, J. B. Wendt and M. Potkonjak, “Security of IoT systems: Design challenges and opportunities,” 2014 IEEE/ACM International Conference on Computer-Aided Design (ICCAD), 2014, pp. 417-423, doi: 10.1109/ICCAD.2014.7001385.

[3]K. Yordanov, P. Zlateva, I. Hadzhidimov and A. Stoyanova, “Testing and clearing the high temperature module error from 0 to 1250°C for measurement with 16 K-type thermocouples,” 2018 20th International Symposium on Electrical Apparatus and Technologies (SIELA), 2018, pp. 1-4, doi: 10.1109/SIELA.2018.8447096.

文献[1]和[3]都做了测温系统，都用了：单片机、热电偶、无线通讯（蓝牙orWifi），总结一下就是使用物联网思维的分布式测控系统。主要学习其分布式系统的设计思路。

文献[1]的主要亮点是可分布式采集的数据存储、传输都体现了物联网思维，方便接入其他物联网系统，可拓展性强。

文献[3]则是用了在一个模块内集成了多个热电偶的方式，“用空间换精度”，具体实现的数学推导没太看懂，不过大体思路就是多点采集，剔除异常值，取有效数据均值以降低随机误差。

文献[2]主要讲了在物联网系统信号传输的主要方式中，如何做好数据加密，具体加密过程涉及到一些密码学的知识，不过其中一条简单的处理思路很受用：在配对再验证成功后传输数据，否则数据存储在安全的本地存储介质或上。还可以加入一个实时匹配检测程序，当物联网设备使用某种形式的通信技术连接到其他未验证渠道时，执行故障安全程序，例如，中断通讯或者启用报警程序。正好用电开发板有接入SD卡，在实现测试系统基础功能后，可以考虑加入这个安全保护措施。

在两篇关于多点分布测控的文章中，都提到了异常值判断的问题，目前做的项目如果采样频率足够高，可以迁移到时域多点异常值去除，当然，即使采样频率不太够这个过程也是很必要的。

基于之前的误差理论知识，剔除异常值有3σ原则、Grubbs检验法、回归分析判断等，文献中使用的方法是四分位距法，这个方法在商务数据分析课程中讲过，但只用了函数库，具体过程没自己做过。

学习了一下，具体的判断过程：按顺序取最后二十个温度读数，并将它们分成三个四分位数。四分位数一（Q1）是数据集前半部分的中位数，四分位数二 （Q2） 是整体集的中位数，四分位数三 （Q3） 是集后半部分的中位数。Q3-Q1计算四分位数Q4范围。最后，四分位数范围乘一个恒定值（这个值取决于你想要多大的有效数据范围）得到IQR(Interquartile Range)，然后有效数据的下限和上限就是[Q1−IQR,Q3+IQR]。如果当前温度低于下界或大于上界，则是一个异常值，给与剔除。

恒定值乘数的设置需要经过试验和错误测试。总体而言，使用四分位数范围的策略在消除可能的离群值方面更为有效，因为边界可以根据给出的数据集动态变化，而不是硬编码到特定值，这种动态变化允许更精确的检测。

此外，在设计软件系统功能时，想给出实时的测量精度，并通过串口进行系统误差的校正，在计算精度时需要实时计算标准不确定度，这个参数在进行3σ检验、Grubbs检验时可以直接拿来用，检验的时间复杂度会比用四分位法低，而且这种检验方法在误差理论中是普遍认可的。

简而言之，如果测试系统在进行实时精密度计算的情况下采样频率满足上升时间要求，则可以使用Grubbs检验异常值，否则不进行精密度实时计算，使用四分位法检验异常值。

最后，给出两篇在知网找到看着还行的文献：

[1]常广晖,常书平,张亚超.高精度热电偶测温电路设计与分析[J].计算机测量与控制,2021,29(03):67-71.

[2]张海涛,罗珊,郭涛.热电偶冷端补偿改进研究[J].仪表技术与传感器,2011(07):11-14.

这两篇文献的内容可以分别用一句话概括：[1]作者用最小二乘法拟合了热电偶温度计算函数t(E),比分段线性法和插值法精度高（存疑，这应该是在插值表密度低的情况下）复杂度还低。[2]作者把冷端补偿电路和热电偶测量电路分开了，因为合在一起不经有补偿电路本身精度影响，还有补偿的线性与热电偶非线性输出间不匹配造成的误差。

这两篇文章最大的作用就是在写一些材料时可以参考其中一些段落，作为众所周知……另外也看了一些其他知网的有关热电偶测温的文章，大多没啥参考价值。以以往在知网查文献的经验，知网最有价值的文章就是各大院校的学位论文，可能最简单的方法就是找做相关课题的学位论文然后参考着做。

【文献学习】热电偶信号调理电路

这篇笔记主要是记录一些文献中，热电偶温度测试系统相关的信号调理电路以及数据处理方式，并稍作总结，在之后做一些测试工作，归并改进，以对初步设计的系统进行升级迭代。

1.用电压—频率转换的方法处理热电偶信号

Murmu, A., Bhattacharyya, B., Munshi, S., 2018. A synergy of voltage-to-frequency converter and continued-fraction algorithm for processing thermocouple signals. Measurement 116, 514–522.. doi:10.1016/j.measurement.2017.11.047

文献主要的亮点是用了Vtof 电压频率转换电路处理热电偶信号，用 continued-fraction algorithm 连续分数算法在MCU中做信号处理。较之后面的其他文献，实现的精度不是特别高，但胜在简单可靠，没有复杂的硬件设计，实现过程也易于理解。

电路用了 负温度系数的热敏电阻，接入LM311的8引脚进行冷端温度补偿，再把带有补偿、热电偶输出的信息的方波输入MCU。

电路图：

电路首先使用三个OP07组成的差分放大器，按照虚短虚断推算，放大倍数为R1/R2,放大后经过一个RC低通滤波滤除工频干扰，然后通过高精度电压频率转换器LM311转换成一定频率的脉冲序列。

输出方波频率与输入电压的关系：
约束条件使得LM311引脚 67 的时间常数匹配
而参考节点的电阻由方波的上升时间τ决定：
再之后，把vout通过采集卡输入进处理器后，就可以由信号的上升时间、频率获得热电偶所测温度了。文献中使用PC声卡采集信号，因为要求输入信号有效值不超过1V所以进行了分压、去耦处理，然后分别使用上升沿触发、下降沿触发得到两个脉冲序列，从而获得τ与f。

在大多数实现线性化输出的技术，多是基于只读存储器 (ROM) 的查找表(LUT) 方法和涉及分段线性或多项式插值的软件方法。基于硬件的线性化方案，特别是模拟线性化电路很少。这是一个很不错的参考电路。
作者在恒温油箱中的测试结果：

2.双输入对数运算放大器处理，用模电提高线性化

A. Mukherjee, D. Sarkar, A. Sen, D. Dey and S. Munshi, “An analog signal conditioning circuit for thermocouple temperature sensor employing thermistor for cold junction compensation,” 2013 International Conference on Control, Automation, Robotics and Embedded Systems (CARE), 2013, pp. 1-5, doi: 10.1109/CARE.2013.6733711.
先看电路图：

冷端补偿：

上面的三运放放大网络的分析没太看懂，但这个作者设计这个电路的初衷是通过模拟电路的方式使得热电偶的输出信号能更具线性度，用这总方式可以实现不用MCU，仅仅通过模拟电路与基础ADC、译码器和显示电路就能完成温度读取。但在我所做的系统中并不想考虑这种方案，因为运放太多了，较多的有源器件会映入更多的噪声，也对电路测试调整带来了很大的困难，而且较之调研的这些方案我觉得我的软件设计能够成为一个亮点。

简而言之就这个电路比较复杂了，有一定的参考价值，但不值得做复现或者改良。

作者通过SPICE仿真验证了在非线性输入与温度补偿，从其他文献以及热敏电阻数据手册获得模拟参数，仿真结果 标准偏差在0.32°C 到 0.76°C ，用实物做的话肯定达不到这个精度。

3.用反向插值表or函数处理热电偶信号

L. Ximin, “A Linear Thermocouple Temperature Meter Based on Inverse Reference Function,” 2010 International Conference on Intelligent Computation Technology and Automation, 2010, pp. 138-143, doi: 10.1109/ICICTA.2010.284.

这个处理电路使用了AD590读取冷端温度，AD转换输入单片机做数据处理与结果显示。

电路示意图：

这个实现比上一个还要复杂，其中冷端补偿的方式也是独具一格：用多路复用放大电路，对热电偶、校准电阻输出信号（U1~U5）进行一定的数学运算从而运算确定0℃电压值，进行零点校准的同时也完成了冷端补偿。这个思路很有特点，但是仔细一想，根本不用做的这么复杂。零点校准完全可以放到MCU里面来做，换一个运算速度更高的处理器，比实现这个复杂电路省钱还省力。

这里用AD590做冷端温度补偿，这个温度传感器在许多教程、课程中都有例举，但查了一下，典型的旧时代外国产品，又贵精度还低，完全是吃了老教材、教程的红利（个人观点），而且我设计的初步方案也有考虑用这个传感器，但是进行传感器调研选型后连买来试一下的想法都没有。

做输出计算，一般是根据标准参考函数或反向参考函数计算温度值。这样可以获得准确和线性的测量。但是，通过微处理器计算的函数比较低效，并且对实时测量有很大的影响。在这篇文献中，作者研究了标准参考表的方法，其不仅可以实现按标准参考功能进行温度测量，而且可以节省大量的计算时间，保证实时测量的准确性。与搜索标准参考表的方法相比，反向参考表的查找方法以热电动力经过简单运算为表地址，节省搜索时间，简化程序，也在一定程度上提高了实时性。

首先复习一下单片机中热电偶信号最简单的处理方法：首先通过冷端温度to 查表找到对应热电势Et，然后加上热电偶输出E2，得到所需要的E(t) 。中间温度定理，上节笔记有提到。

这里作者做了一件我认为非常有参考意义的事：他对比了多项式拟合法和参考函数表查找法的精度匹配情况：

计算后发现，对数据进行九阶拟合的精度

对比： 0 ~ 50℃的参考表E ( t ) 51个数据

-200 ~ 1372℃的反参考表t ( E ) 2026个数据

这两个表的查询、插值精度是和多项式拟合计算的结果相差不大的（甚至表做的数据够多，间隔等于Et分辨率时都不用插值）

这里作者做的反向差值表 ，温度区间根据测量不同决定，把计算得的热电动力E(t) 除以反向参考表的间隔（文中是30uV），商数乘以 2 作为查找表的地址，可以直接获得温度测量。根据存储空间的大小，对逆参考函数表t [ E ( t , 0 ) ]进行尽可能的扩展，以获得尽可能高的测量精度。

而在MCU中计算一个九阶多项式，花的时间是非常多的，使用ROM存储查询表，地址搜搜查找的方式， 明显后者复杂度更低。这是一种用静态内存换取运算速度的方式，考虑到我目前使用的STM32 512Kb内存，存三五千个数据的查询表完全够用（虽然这会对后面接入微处理器操作系统造成一定影响，不过开发板带了SD卡，大不了存SD卡，用的时候放到闪存里面），我会在后续的系统迭代中使用这个数据处理的方法。

此外，这个通过热电势的值简单运算得到查找表地址的思路，和有序向量插值查找的思路十分相似，甚至可以说如出一辙。而文献中的这种查找方式有很大的局限性：它必须要求查找表按照Et等间隔、在测量范围内全部有序的给出，这导致，如果想要提高查询表密度以提高精确的，就得全面地提高查找表的密度，占用更大的静态内存。虽然提高密度不过是在生产查询表的程序中改一个参数而已，不过占用内存总归不大方便。基于此，我准备利用有序向量插值查找的思路，对这个查找方法进行改写，实现在loglogn的时间复杂度内（这是非常低的了）实现Et到t 的查询、插值，且不必要求查询表等间隔分布，可以在重点测温范围内大密度做表，在其他地方小密度做表。

##4.基于递归B样条最小二乘的方法给出拟合函数
Guo Wei, Xin Wang and Jinwei Sun, “Signal processing method with cold junction compensation for thermocouple,” 2009 IEEE Instrumentation and Measurement Technology Conference, 2009, pp. 1458-1462, doi: 10.1109/IMTC.2009.5168685.

作者用一种基于递归B样条最小二乘的方法作为解决方案 ，生产两个计算模型E(t) 、 t(E) ，来消除冷端干扰并计算热电偶热电势到温度转换。

采用 B 样条最小二乘法是因为它的近似质量很好。递归方法用于简化操作并使其适合在MCU中使用，所以就可以实时的在MCU中进行模型的校准（热电偶使用久了，要是不是校准标定），而其他的计算模型，无论是最小回归、查询表法，都得测得数据后在计算机中建立计算模型。这点是这篇文章所用方法的最大两点。

测试结果：

S型相对误差为0.45%，K型为0.29% 。作者仅使用热电偶标准表的模拟研究 ，但是没做实物。

再提一嘴，这些文章提到所做测试系统的精度时，用的标准都没有统一。这篇文章给的参数是最大相对误差和平均相对误差（做异常值判断了吗，给的是平均值与参考值的相对误差的话，需要给出测试点数啊），而其他文章有的给精度Accuracy（给精度要给置信区间啊），有的给绝对误差，有的给均方根误差（这个好），这对各方案的精度横向对比造成了很大的困难。

之后我写的各种报告，精度确定规范尽量按照国际计量标准来。

【信号处理】一种热电偶信号处理算法

热电偶信号处理，无非两种方法：
插值法：插值表密度决定精度；复杂度集中在搜索插值点
拟合法：数据密度和拟合方式决定精度；复杂计算耗时大；实现更容易

因为在所设计系统应用中，需要更新插值表，而再导出到PC软件中做拟合，太麻烦（在MCU中实现的拟合也有，例如之前文献学习提到的基于递归B样条最小二乘的方法给出拟合函数，但在单片机里写还是太难了），所以考虑用插值方法。

插值方法时间复杂度主要集中在插值地址搜索，在之前学习的文献中有一种方法：分度表等间隔分布，通过热电势的值简单运算得到查找表地址的思路；这和有序向量插值查找的思路十分相似。

L. Ximin, “A Linear Thermocouple Temperature Meter Based on Inverse Reference Function,” 2010 International Conference on Intelligent Computation Technology and Automation, 2010, pp. 138-143, doi: 10.1109/ICICTA.2010.284.

而文献中的这种查找方式有很大的局限性：它必须要求查找表按照Et等间隔、在测量范围内全部有序的给出，这导致，如果想要提高查询表密度以提高精确的，就得全面地提高查找表的密度，占用更大的静态内存，而且需要E-t，t-E两个表。

基于此，我准备利用有序向量插值查找的思路，对这个查找方法进行改写，实现在loglogn的时间复杂度内实现Et到t 的查询、插值，且不必要求查询表等间隔分布，可以在重点测温范围内大密度做表，在其他地方小密度做表:

用MATLAB实现，因为之后可能要配合Simulink做模拟电路、数字数据处理的联合仿真：

先自己写一个插值函数，之后移植到单片机需要改写成C语言：

function [index,Tout] = insert_search(indextable_T,indextable_V,Vin)
    Vsearch=Vin-indextable_V(1);
    id1=Vsearch/(indextable_V(end)-indextable_V(1))*length(indextable_T);
    index=fix(id1);
    if index==0
    stepT=(indextable_T(2)-indextable_T(1));
    stepV=(Vin-indextable_V(1))/(indextable_V(2)-indextable_V(1));
    Tout=indextable_T(1)+stepT*stepV;
    return
    end
    while Vin<indextable_V(index)||Vin>indextable_V(index+1)
        if Vin<indextable_V(index)
        Vsearch=Vin-indextable_V(1);
        id1=Vsearch/(indextable_V(index)-indextable_V(1))*index;
        index=fix(id1);
        elseif Vin>indextable_V(index+1)
        Vsearch=Vin-indextable_V(index);
        id1=Vsearch/(indextable_V(end)-indextable_V(index))*(length(indextable_T)-index);
        index=index+fix(id1);
        end
    end
    stepT=(indextable_T(index+1)-indextable_T(index));
    stepV=(Vin-indextable_V(index))/(indextable_V(index+1)-indextable_V(index));
    Tout=indextable_T(index)+stepT*stepV;
 
end

这里用到的插值搜索的思想：

插值得到大概的index，再判断Vin是不是在Vsearch[index，index+1]内，是的话直接线性插值，不是的话再判断是大了还是小了进入[index,end]或者[1,index]递归处理

考虑到所做系统对快速性的需求，所以改写算法的时候把最初的递归改成了while循环迭代，减小了函数栈开销。

测试程序：

clear; clc; close all
 
indextable_T = xlsread('K型热电偶分度表.xls',1, 'A3:A143'); %in ℃
indextable_V = xlsread('K型热电偶分度表.xls',1, 'B3:B143'); %分度表数据导入,in mV
 
V_in=input('模拟热电偶输出电压 -0.392~51.82: ');
T_in=input('模拟冷端补偿温度 -0~1370: ');
[indexT,Tout] = insert_search(indextable_T,indextable_V,V_in)
[indexV,Vout] = insert_search(indextable_V,indextable_T,T_in)
 
V_tc=(indextable_V(1):0.1:indextable_V(end));
T_tc=(1:length(V_tc));
for i=1:length(V_tc)
    [~,Ttc_now]=insert_search(indextable_T,indextable_V,V_tc(i));
    T_tc(i)=Ttc_now;
end

如果输入定值的V_in或者T_in,可以看到大多数时候2~4次搜索就可以找到地址了，这个效率是非常高的。

再检查输出更高密度V_tc分度表，看上去没什么大问题

V_tc(256) = 25.5000

T_tc(256) = 614

观察原分布表，输出值比较合理

异常值处理和分度表更新

异常值处理会的有以下方法：

3σ检验、Grubbs检验法： 这需要实时计算标准不确定度，之前写在STM32里的不确定度计算函数，由于sqrt函数实现的不够好，总体效果不是很满意，而且单片机里面 u8 char，u32 int float 和ADC转换的二进制数 相互运算、处理，总不知道哪一步是没转换还是怎么的，例如：

从温度传感器DS1820读取的一字节二进制数：

DS18B20_Read_Byte()
{
    u8 data;
    for (i=1;i<=8;i++) 
        {
            j=DS18B20_Read_Bit();
            data=(j<<7)|(dat>>1);
        }
    return data		
}

u8 temp,TL,TH;
TL=DS18B20_Read_Byte(); // LSB   
TH=DS18B20_Read_Byte(); // MSB  
                    
tem=TH; //获得高八位
tem<<=8;    
tem+=TL;//获得底八位
tem=(float)tem;//转换

这样从存储器读取一个十六位二进制数，然后转到了 u32 float，32位单精度浮点数。之后如果和double、int之类的做运算，是不是都要先把两边转成float，例如：

float f = 3.4 这样就是double3.4 应该写成： float f = (float)3.4或者写成 float f = 3.4f，总之标准差计算过程还需要进一步完善。

四分位数法：
四分位数一（Q1）数据集前半部分的中位数
四分位数二（Q2）整体集的中位数
四分位数三（Q3）集后半部分的中位数
Q3-Q1计算四分位数Q4范围，Q4乘一个恒定值得到IQR(Interquartile Range)
然后有效数据的下限和上限就是[Q1−IQR,Q3+IQR]

使用四分位法不用计算标准不确定度，会比较快一些，但是因为有效范围是自定义的，就是说不想σ或者Grubbs法这样确定异常值的把握有多少（99.75%，比如）

---

分度表更新，有两个问题：

一是选用何种数据结构存储分度表，二是如何改变本地存储，就是变了之后单片机reset一下数据不会复原。存flash感觉不太安全，所以存了sd卡。

至于分度表的数据结构，简单的两个数组我觉得是不合适的（虽然这最简单而且常用），考虑到分度表更新，数组的话更新限制太大，在一个位置插入T，就要在另一数组相同索引加入E，插入过程也就是后面挪一下，但是数据安全完全没有保障，就是说如果在更新的时候出了一些意外，比如insert(T,E）,T不小心输大十了十倍，存最后去了，那E是跟着T的索引还是自己再寻找插值地址?

如果是E跟着T索引，那要改正只能说在数组里进行delete(T)，删除，后面全部前移，再delete（E）,如果不想这么复杂，在插入的时候得加一个判断，判断E跟着T的插值地址，其插值表两边的值是否合适。 这使得更新的逻辑特别复杂。如果是E，T分布自己寻找插值地址更新，那就失去了单调检验的功能：输入的（E，10T）分别插值到不同的索引，那么也是得定向delete刚插入的，没有发现插入错误的话就得重新制表了，这非常的不合理。

更新困难只是一小部分，另一重要原因是：如果存储的数组被不小心错误更改（因为要提供更新表的功能所以肯定要做修改的接口），例如 E T 两个数组删了索引没对上的一组元素，那么整么表在某个索引后就是错误的了，而且这种情况也能通过顺序排列检查！

概括：把分布表做为两个数组结构不适合更新，其不仅跟新复杂，而且安全性没有保障。要保障安全、可靠，需要非常非常复杂的逻辑判断防止错误操作，注意事项太多，很容易出问题。

改进的方案，一是做一个struct结构、Binary Search Tree结构或者 Class:ThermocoupleData ，每个元素(节点)存两个float数据和指针。 如果是struct结构可以用指针数组指向n个struct，完成分度表建立；如果是二叉搜索树，直接用搜索树Class模板，然后改一下树节点状态即可。

用指针数组的好处是分度表在struct内严格一一对应，这样数据安全有了保障，无论如何不会出现错误对应的数据。而插入、删除、搜索的复杂度都是和数组类似的；用二叉树结构存储，看起来更厉害一些，而且插入、删除、搜索都可以在log(n)复杂度内实现，但是上面写了半天的向量插值搜索就白写了。而且一个麻烦是Class 是C++适应，转成C头文件也挺累的。

最后使用的数据结构方案是：用datastruct+指针vector 存储分度表。