【数值分析】课程学习_上
Hi,这是数值分析课程中的笔记。
原文档
基础概念&线代复习
计算机中的浮点数计算:
表示:
x = (−1)^s ·(0.a_1a2 ···at ) ·β^e = (−1)s ·m ·β ^e−t
符号位、有效位数、字长 ~ 在存储中为符号位、阶码、尾数位
类似于科学计数法
和之前学的二级制浮点数表示有点相似,但又不完全相同
Matlab 默认的数据类型是 double
向前误差分析 f(x∗) = (x)2(1 + 2δ) ;f(x)=x^2
向后误差分析[f (x)]∗ = f (x(1 + ̃δ))”
条件数:|f (x + δx) −f (x)| /|f (x)| ≤ κ(x)|δx|/|x|
κ(x) 自变量变化引起函数值的变化 类似于灵敏度 太大是病态的
κ(x)= |xf ‘(x) /f (x) |
避免相近的数相减 会严重损失有效数字
避免和绝对值大的数相乘、和绝对值小的数相除
减少运算次数: x3 −6.1x2 + 3.2x + 1.5 -> ((x −6.1)x + 3.2)x + 1.5
选公式: ln(1+x) ln(1+x/1-x) 的 Taylor 展开算 ln2 后者强
MATLBA - norm 求范数
矩阵的 1 范数是列向量绝对值和的最大值;
无穷范数 是 行向量绝对值和的最大值




线性方程组的直接解法
下三角方程的解法:

向前迭代 复杂度 O(n^2)
上三角方程算法差不多,复杂度同样量级
高斯消元
本质上是找到一个非奇异矩阵,使得 A=LU LU 分解
算法复杂度是 O(n^3);迭代的过程 相当于每次左乘一个单位向量 l=(0,0,…ak+1/ak…an/ak)。
A=LU Ly=b Ux=y
非奇异矩阵,若顺序主子式均不为 0.则存在唯一 LU=A,分解唯一; 顺序主子式 det !=0 保证第 k 步的 akk!=0. 如果遇到—选主元?
如何作 LU 分解?
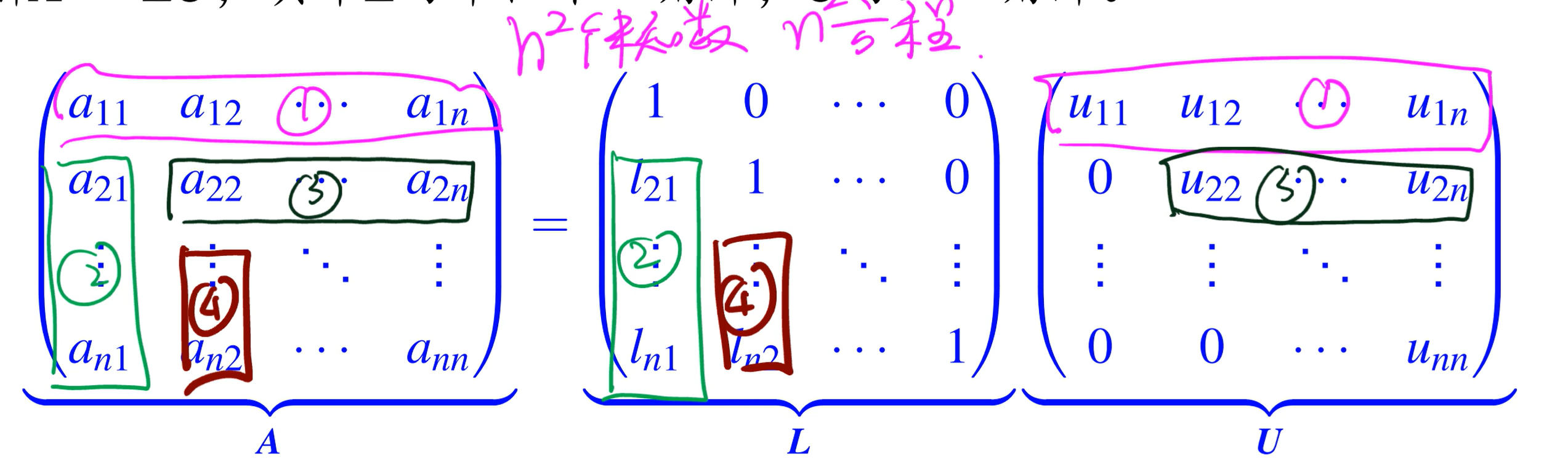
A 的第一行 等于 L 的第一行 × U 的每一列 先让,A 的第一行和 U 的第一行是相等的。
然后 A 的第一列, = L 的每一行 × U 的第一列。注意 u11 已知了,所以可以直接求解出 L 第一列
之后就如此往复,求 U 的 i 行、L 的 i 列
doolittle 分解算法:

就是上面的,往复求 U 的第 k 行、L 的第 k 列。
[L,U]=lu(A) MATLAB 分解
一些特殊矩阵的分解可以优化:例如三对角矩阵。
参考一维 poisson 方程的求解,使用数值解近似,就会需要求解一个三对角矩阵。

u1=b1; li = ai/ui−1 ; ui = bi − lici−1,
追赶法 复杂度 On; amtlab 接口 Thomas
如果是循环三对角方程,也有对应的计算方法。

Gauss 消去:对角元素等于 0 或非常小的情况。
选主元:在解到第 k 步时,选 akk–ank 中 最大模的元素与 akk 进行交换行。
在每次消去前,选主元,换行。是一种牺牲复杂度换取更高精度的方法。
即:存在排列阵 P ,使得:PA=LU
[L,U,P]=lu(A) matlab 计算方法,会默认给你选主元。如果输出不带 P,会给你 × 进去。
cholesky 分解
分解时,U 可以再分解成 DU* 对角阵 D 和单位上三角阵 U*
若 AT=A 对称矩阵;则存在单位下三角矩阵: A=LDLT 利用特殊矩阵的性质,尽可能减小计算量。
正定阵: A 存在唯一的 对角元素为正的 下三角阵 L A=LLT (L~=LD^1/2 不是单位下三角了)
在设计算法时,利用 U=LT,可以进行一定的计算简化。

cholesky 分解,也就是正定对称矩阵的分解,可以检验对称阵 A 是否正定。能做完这个算法就是正定的
MATLAB 函数 chol(A),A=R’R
可以通过线性方程组求解的方法求矩阵的逆。
X 是 A 的逆矩阵,则 AX=I Axi=ei ,A 乘上 X 的每一列,等于 I 的对应列
条件数
在直接法求解线性方程组的过程中,由于舍入误差的存在,微小的扰动可能造成解很大的变化。

所以定义了一个条件数,来描述解的变化随扰动的变化情况:

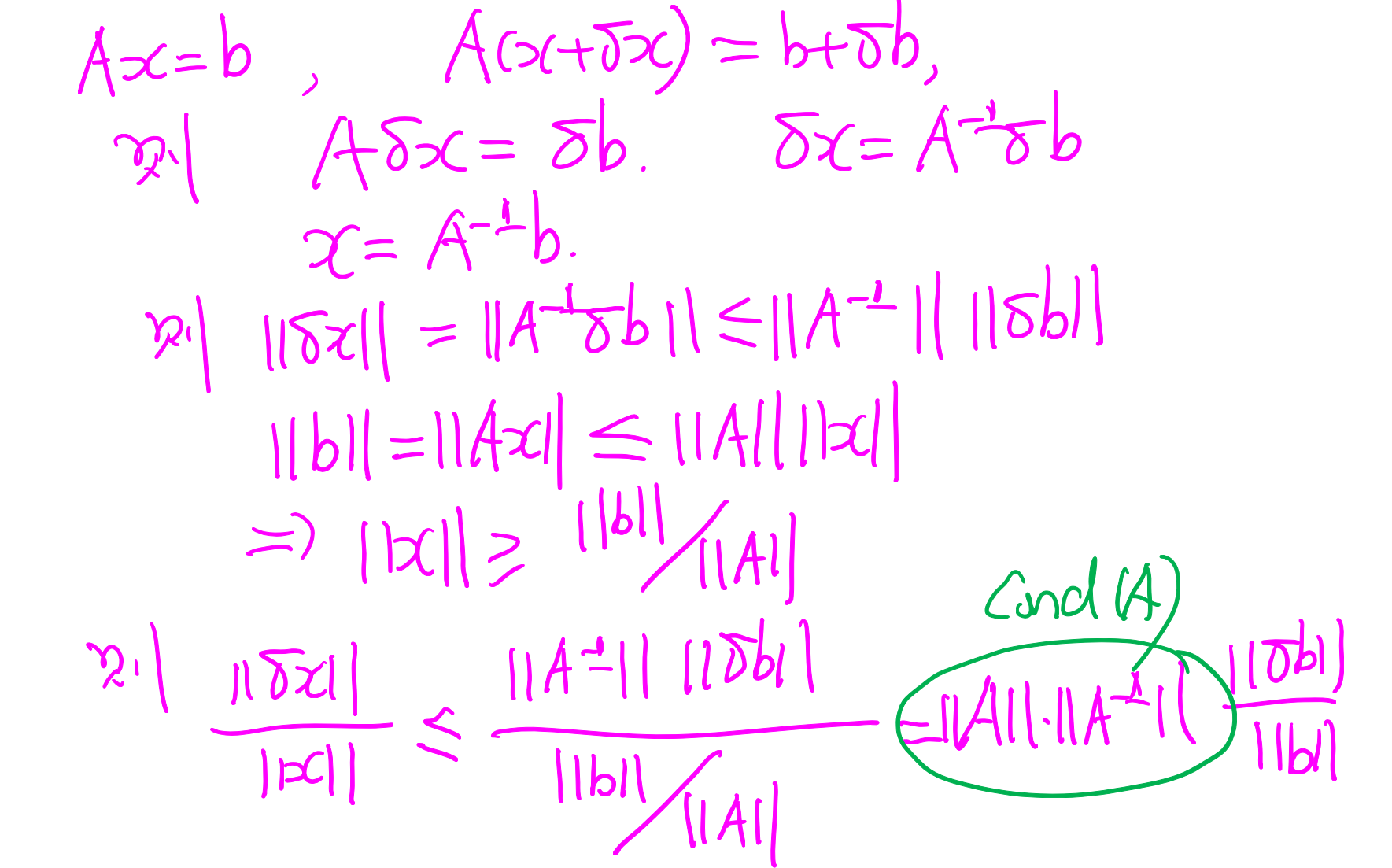
矩阵条件数-计算机计算数学中产生的问题,

具体如何通过 COND A ,还不太懂。。常用的是 2 - 1 -∞ 范数。
计算机总是存在舍入误差,所以算的是 (A+δA) * (x+δx) = (b=δb)
b!=0,且 δA 够小,使得 ||A-1||||δA||<1 有:
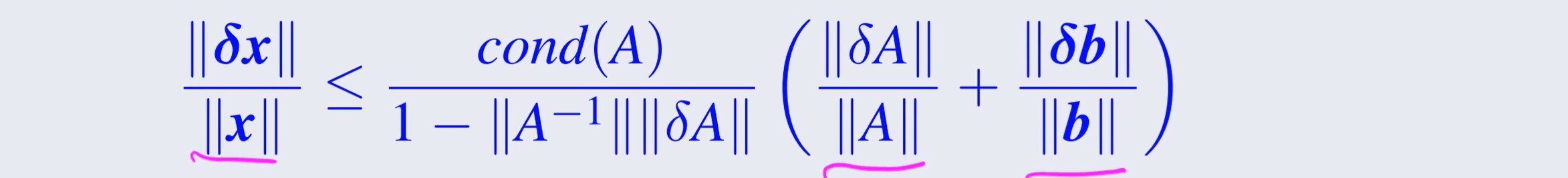
性质:
condA>=1;condA=condA-1 ,
condαA=condA
若 A 为正交阵,ATA=I ||A2||=1 cond2A=1
若 U 为正交阵 cond2AU=cond2UA=cond2A
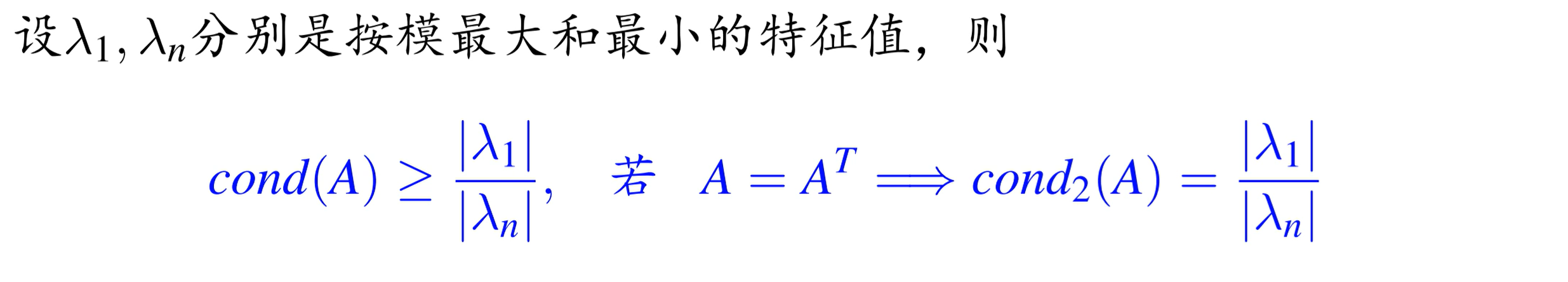
condA>>1 则是病态的;条件数的值与范数的选取有关。
MATLAB 命令 cond
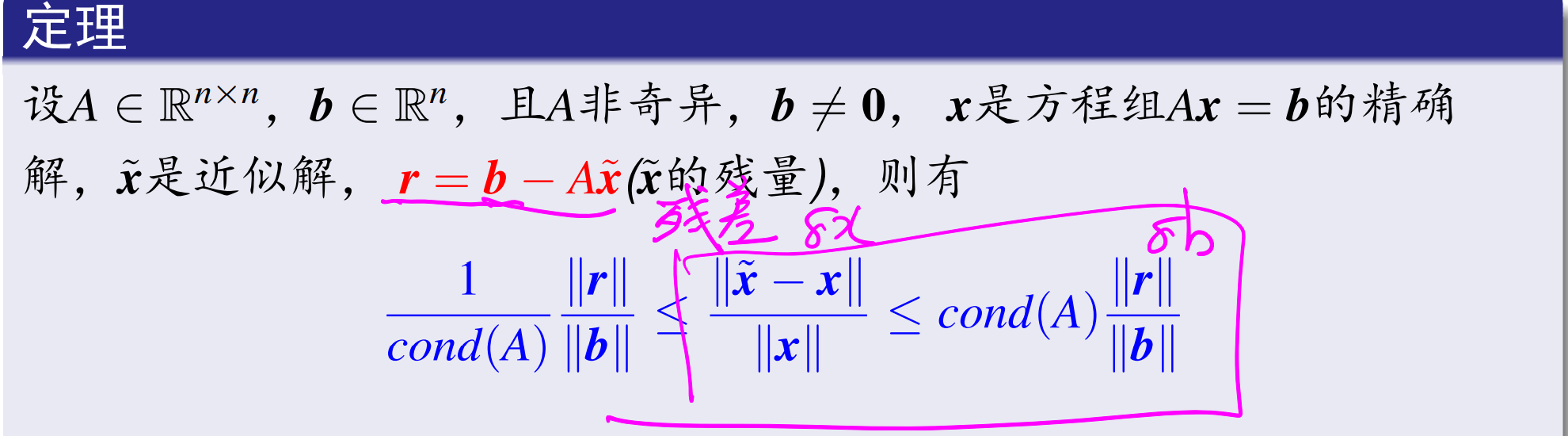
可以使用可计算的 r,去衡量计算结果的精确度。残差的大小去衡量解的误差。
需要注意的是,使用 r 衡量解的 δx 时,需要 condA 不是病态的。
矩阵的条件数和行列式没有必然的联系,病态的出现主要是某些列向量近似线性相关了。
粗略地说,如果用主元素法或平方根法解方程组,设 A 和 b 的元素准确到 s 位数,且 condA=10^t,t<s,则计算的解向量大约有 s-t 为有效数字的准确度。
预处理
一般会做一些预处理,把 condA 降下去。
可以考虑矩阵的行列分别乘上不同的 const,即寻找可逆对角阵 D1 D2(左行右列),将方程组 Ax=b 变成:
D1AD2y=D1b ,x=D2y
理论最优: min cond(D1AD2); 通过计算量来优化精度。
非线性方程组的迭代解法
迭代法思路
45° 卷,卷也卷不动,躺也躺不平;
很多时候的数学问题都是优化问题-find min。常见的:如果能找到函数的下界,可以构造一个单调递减的序列,主要是迭代的函数,让序列逐渐逼近目标 min。所以迭代法的关键就是找到迭代的函数,让序列以一定方法逼近目标值。
如果带有约束,可以引入 lagrange 乘子把约束融入目标函数,变为无约束问题。
解方程组的更,采用不动点迭代。
ax=b ==> ax-b=0 ==> 1/c(ax-b)+x=x,不动点代换 G(x)=x+1/c(ax-b)
通过一定的迭代方法, 使目标序列逐渐逼近不动点。
序列收敛:简单的求极限

注意,Jacobi 矩阵 各偏导都存在,向量值函数不一定可导。

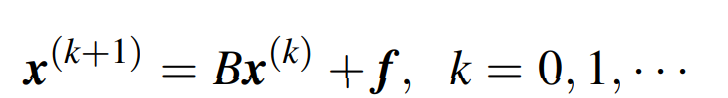
本课程基本都是使用的 线性 定常 单步迭代-即最简单的迭代公式。
收敛阶:形容方程组在多少阶次下的收敛性质

就是说收敛的阶次高低。本课程线性方程组基本都是 P=1。有给结论:P=1 线性方程组的迭代收敛性不依赖于初值的选取。而非线性方程组一般是没有全局收敛性的,所以一般要选取到充分靠近解 X*的初值。初值的选取不同是两种迭代方法最大的区别。

某个作业题用到了这个性质。
非线性迭代需要一个迭代终止条件:r^(k)<ε (非病态) ; x(k+1)-x(k)< ε (超线性收敛) ;max 次数 N
方程组求根问题,等价转化位映射不动点问题。
为什么一定要不动点迭代?不动点迭代的方法比零点迭代更加简单吗?在构造不动点迭代的时候,本身就有了一个迭代公式 G,只要再考察 G 是不是压缩的就可以了。

ax=b == ax-b=0 == 1/c(ax-b)+x=x,不动点代换 G(x)=x+1/c(ax-b)
压缩映射依赖于范数选取。那如何判断是不是压缩的呢?不懂 nie,所有的范数都满足压缩条件才,还是某个范数满足即可?
理论基石:压缩映射原理

所以,有压缩映射-》找到不动点 -》迭代求解线性方程组
证明:构造 x(k+1)=G(k) ;证明 x(k)收敛,然后即可证明 lim x(k)=G(x) ,唯一性设俩不动点,他们相等即可。满足压缩映射即可收敛–
F(x)=0 等价到一个映射问题,再构造一个不动点迭代,即可保证收敛。映射只需满足:压缩、内映射。局部收敛情况:找到的 G 在 D 的子域,x 的领域内 ,内映射 ,则可以在 S 内找到不动点,x 称为 S 吸引点,S 为 x 吸引域。 – x 局部收敛。
在实际应用中需要考虑收敛域吗?好像没怎么考虑过-起始点都是题目给的,如果没给一般就取零向量

意思是在判断不动点吸引域的时候, 计算 G‘x*的谱半径比计算压缩条件更简单,这个是可以严格证明的。所以谱半径怎么算? λI-A=0 ,求 max λ ,哪里简单了
也可用用缩放,谱半径小于无穷(1、2,any)范数 简化
上面只教了如何验证迭代矩阵函数 G 是收敛的,但是如何构造还是有说法的,凭空构造不太合理。接下来的介绍的一些方法就是讲如何构造 G
Newton 迭代
不求逆 解方程 LUΔx=-Fx

基本原理:长得很像是 taylor 展开。然后 X*=X(k+1)-最后一次迭代。
G=x=x-F’x^-1 Fx; 不动点等价于 Fx*=0;
所以迭代过程:F’x(k) Δx=-Fx(k)
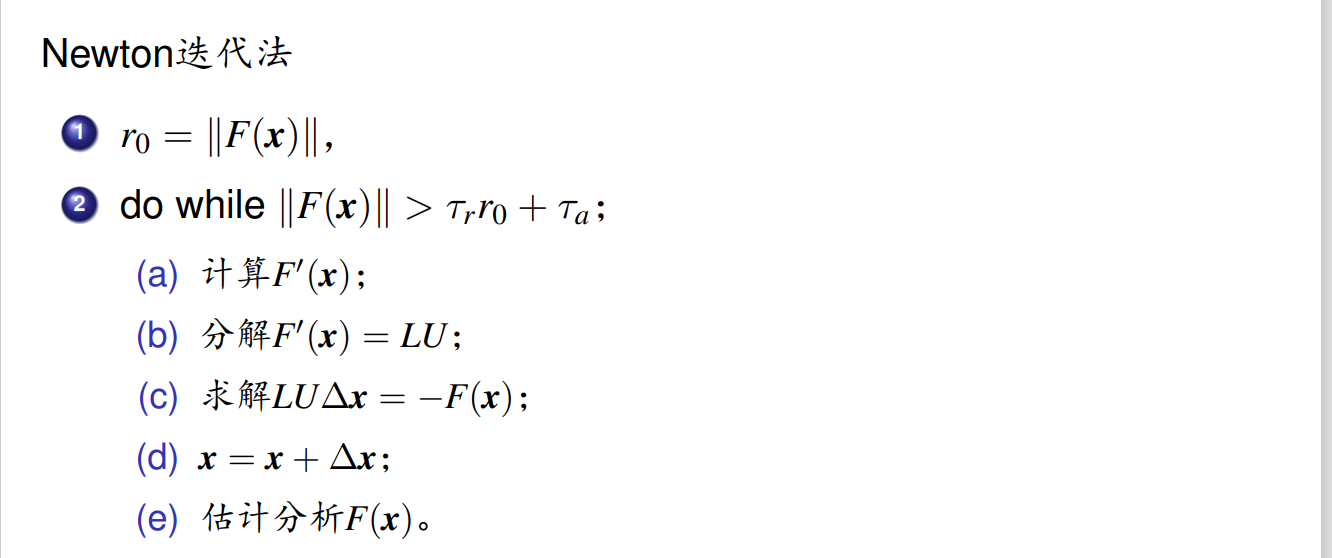
收敛条件:

也记不住。主要就是说,至少是超线性收敛,满足–连续还平方收敛,收敛速度快。
Newton 迭代第一第二步计算量很大,
可以考虑用 F’(X0) 代替所有的 F’X – chord 方法;但是只能求解线性收敛的方程组。
一种折中的方法:m 次迭代更新一次 F‘x Jacobi Shamanskii 方法 ;m+1 阶收敛,能保证超线性
在 F’x 非奇异或者病态时候使用的。遇到 F‘Xk 奇异或严重病态时 使用阻尼 Newton 法

这保证 F‘不理想的时候也能继续算的。引入一个阻尼参数,让其非病态奇异;阻尼的作用类似于往同一个方向慢一点迭代,以避免病态带来的过大误差。
离散 Newton,其实就是超短步长 h,数值逼近 Jacobi 矩阵。
需要注意的是,相较于一般的求微分方法,这里没有使用 1/h[F(x+h)-F(x)] ,这是在避免两个相近数相减破坏有效位数
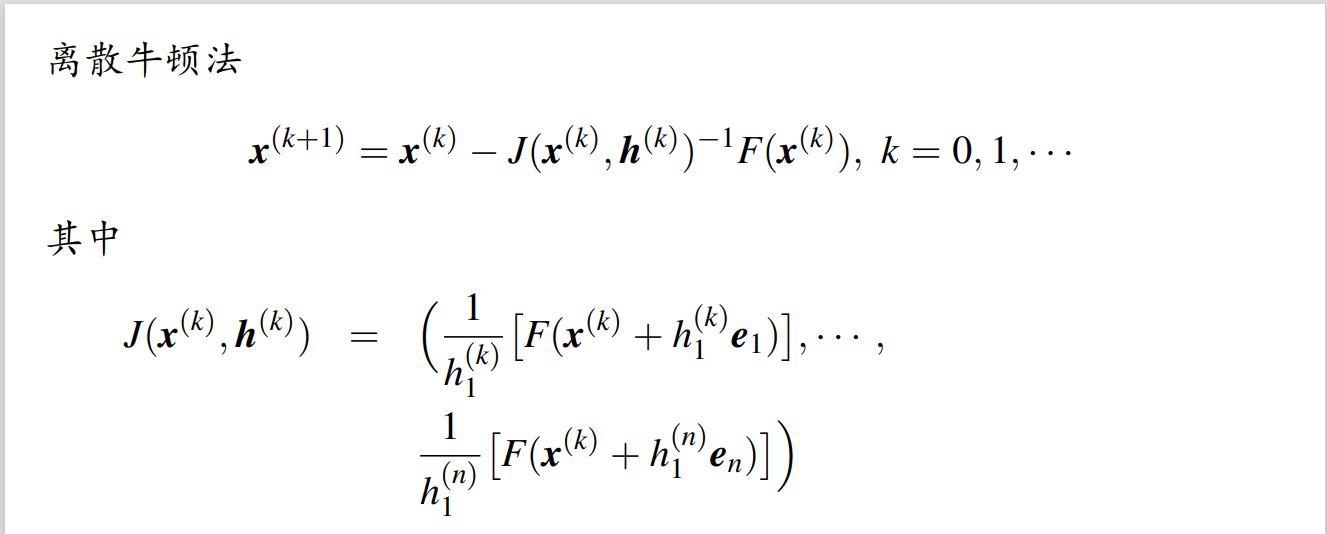
取 hk=Fxk 则收敛速度是二阶;在数值微分时,条件数和步长 h 成反比。
线性方程组的迭代解法
线性迭代思路
之前直接求解线性方程的方法是针对满矩阵设计的,但是实际问题中的 A 一般是大型稀疏矩阵,直接法并不适用。所以可以设计适合于稀疏版本的直接法,用迭代法(基于稀疏矩阵的)来求解。
稀疏矩阵 LU 分解后不一定稀疏。所以需要建构对应的算法
邻接矩阵 – 填充效应
MATLAB 函数 对称正定阵 pcg preconditioned conjugate gradients method
bicgstab biconjugate gradients stabilized method
gmres_ generalized minimum residual method
colamd_ 线性方程直接解;重排可以减小填充效应,但是无法避免 ;
考虑直接迭代法
线性方程组的迭代解法,思路还是转换成某个方程的不动点求解问题。
为什么要有一个 Q 呢?为什么不是(A+I)x-b=x 呢? – 因为需要构造相应的迭代矩阵 B 是吗,Q 非奇异是构造的条件。Q=I 就是最简单的迭代方法。

线性方程迭代法,可以变换成 Bx+f=x ; f 是线性映射。 (I-B)x=f 有唯一解,I-B 可逆; 这仍然是一个不动点迭代问题。
收敛的条件:B 的范数小于 1,且 B 的范数越小收敛越快。

实际应用时大多是求谱半径 <1,收敛速度也与谱半径息息相关。

可以看到解的收敛速度是和矩阵范数相关的

最后用谱半径作计算,是因为:

就是说,计算的收敛速度是 k 区域无穷时候的平均收敛速度。渐近收敛速度
J-GS 方法
这几种方法主要区别在于迭代矩阵的构造。考虑矩阵的分裂:
A=M-N B=M^-1N , f=M^-1b
常用的分裂方式:A=D-L-U 分解成对角阵、严格下三角、严格上三角
jacobi 迭代方法中,M=D,N=L+U ; Bj= M^-1N=D^-1(L+U)=I-D^-1A f= D^-1b

GS gauss-seidel 方法:
和 Jacobi 方法不同的就是每迭代更新一行,下一行就用新的值迭代。表现在迭代矩阵上就是:
M=D-L N=U
BG= M^-1N=(D-L)^-1U=I - (D-L)^-1A

一些特殊矩阵的收敛:对角占优
对角占优矩阵:对角线上的元素绝对值比非对角线上的都大,>=;严格对角占优-都是严格大;弱占优-有一些可以取等,则非奇异
不可约若对角占优,非奇异 ;不可约是啥玩意—如果存在一个排列阵 P 使得 P’AP 为一个分块上三角阵,我们就称矩阵 A 是可约的,否则就称该矩阵是不可约的。
上面的两种矩阵,J 方法和 GS 方法收敛。
证明方法,想办法证明 ρ<1
A 对称,对角元为正; Ax=B
J 方法收敛的充分条件是 A 以及 2D-A 均正定
GS 方法收敛的条件是 A 对称正定
SOR-方法
使用系数 ω 加快收敛速度

体现松弛因子思路的式子:x(k+1)=ωX(k+1) +(1-ω)x(k) ,ω >1 加速迭代;ω∈(0,2)

只需要背一个 M 的形式,由 GS 方法 D-L 变化而来:
$$
M=1/ω(D-ωL) ; N=M-A=1/ω[(1-ω) D+ωU]
$$
迭代矩阵:B=I-M^-1A
对阵正定阵-ω 在 0-2 收敛 证明过程:—- 利用对称、正定的性质,证明构造的任意对称正定阵的 SOR 迭代矩阵 λ<1
最有松弛因子:
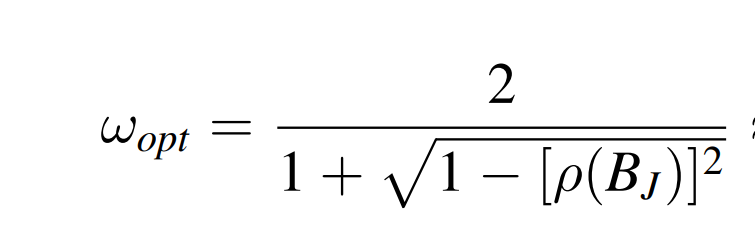
构造迭代矩阵的过程,相当于在构造迭代思路中的 Q-1,预处理矩阵。

在计算迭代法时,一定要避免矩阵相乘和求逆;总之可以通过各种方法换算成矩阵 × 向量。
编程和手算时候,使用迭代法求解大型稀疏矩阵问题,要避免求逆、矩阵乘法等复杂操作。
共轭梯度法
共轭梯度法(一):线性共轭梯度 - 知乎 (zhihu.com)
比经典方法更快的一种方法, 基于变分–求解方程组的问题等价转化成求解一个特殊的二次函数最小值问题。有一个很大的限制:要求 A 是对称正定。

第一个性质是求下降梯度的关键,也是下降向量 r 的来源。第二个性质在推导最速下降和共轭梯度时中会用到。

最速下降法只保证沿着一系列正交的方向寻找最快的下降方向,最快找到 φxmin
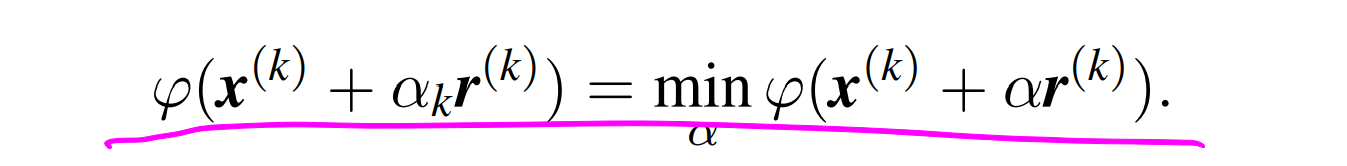
寻找实数 αk 是由微分=0 得到的。

这个方法应该不考吧,由一些硬缺陷,也背不下来。。
性质:相邻两次的搜索方向是正交的;φx 存在极限;k 次迭代后误差的能量模会变小;
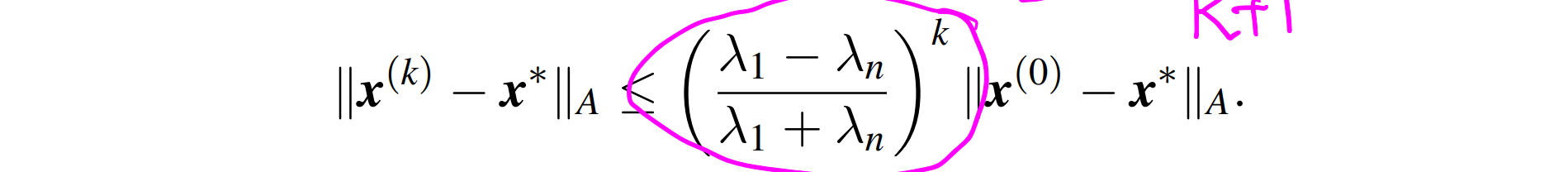
上面的式子说明了最速下降法总是收敛的,但是当 λ1>>λn 时,收敛速度会非常慢;而且 rk 很小时,舍入误差太大,所以这个方法在实际计算时很少应用。作为共轭梯度法的启示–
共轭梯度法-conjugate gradient
思想和最速下降类似,还是一维极小值搜索,但是搜索的方向不再是 r 正交方向,而是选另一个方向 p;p 的选取有说法了:

总之,结论就是 p 序列需要

满足 A 共轭

在使用过程中确定 p(k+1) 基于 pk=rk+β(k-1)p(k-1) ,即取 rk 和 pk-1 的线性组合。
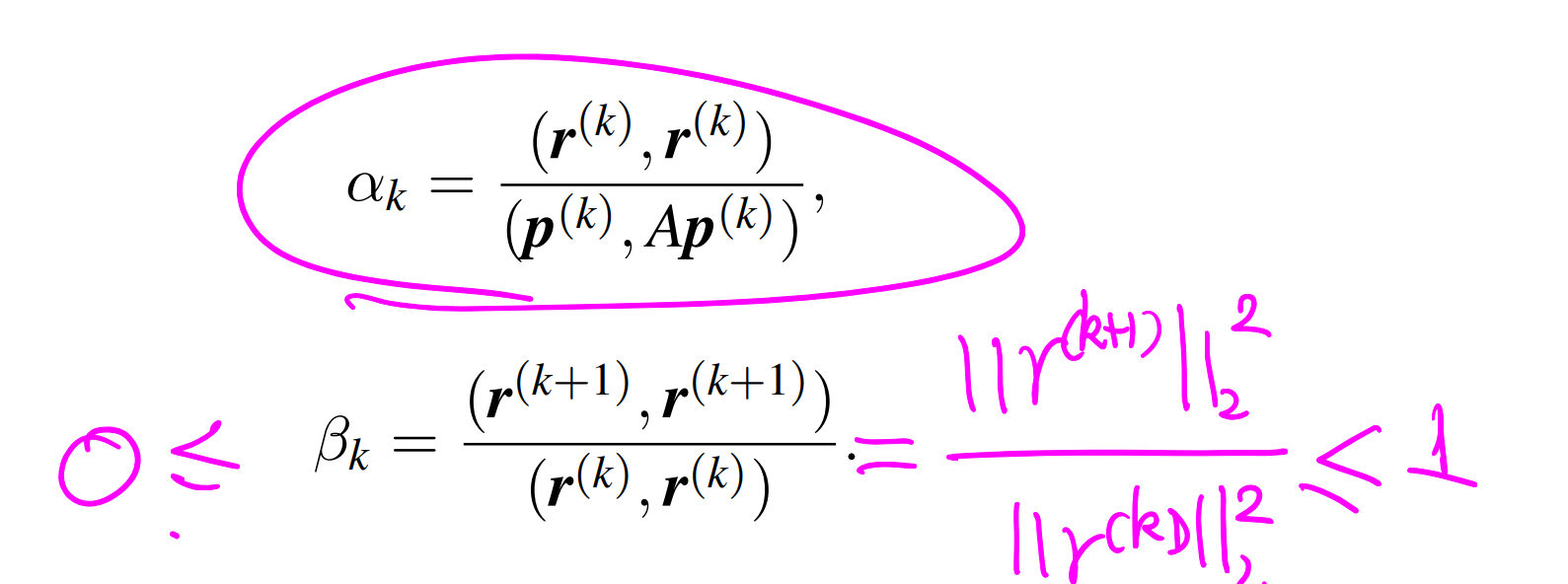
一些有用的性质,证明题可能用到:
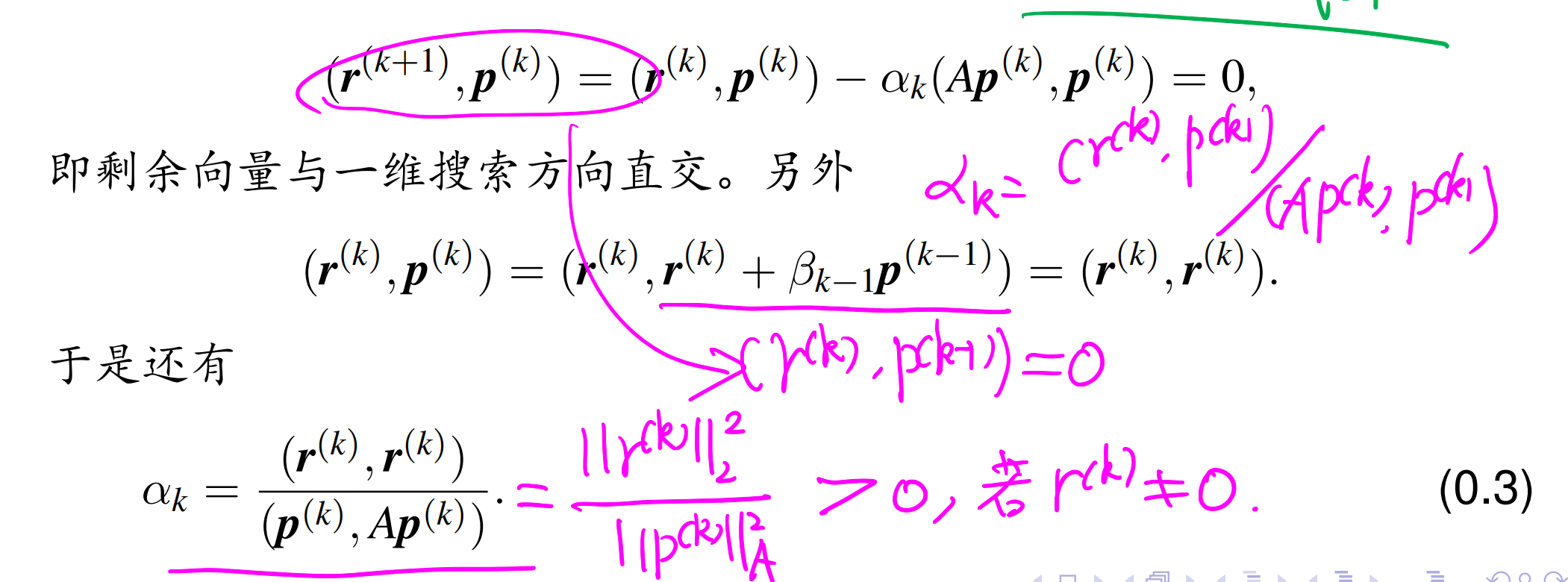

具体的算法:

md,这么长怎么记得住啊
相较于其他线性方程组的迭代解法,CG 法最大的优势就是至多 n 步可以求解,一般情况下收敛速度都会很快的。例如在解二维大型泊松方程时
共轭梯度也有预处理:和直接法类似,把条件数弄小。不同的是,CG 方法的预处理中,需要处理后的矩阵还是对称正定的。体现在具体算法上就是

更记不住了。。其中 M 是预处理矩阵,M=LLT;z 是减少计算次数的中间变量。
matlab 函数 pcg
代数特征值
一般不通过直接求解特征多项式的值来求特征值,(虽然我平时都是这么做的)
一般的方法是通过求友矩阵的特征值(他们特征值相等),而友矩阵的性质比较好 ;可以把一个高次代数的求根问题,转换成求一个稀疏矩阵特征值问题。

圆盘定理:估计特征值所在的范围,矩阵的 n 个特征值均落在 n 个圆盘上,n 个圆盘是复平面上以 a 对角元为中心每一行非对角元绝对值之和为半径的圆盘。这规定了特征值的取值范围,但是范围有些过大,即很多圆盘都可能没有落有特征值。

就是说 λ 落点有对应的区分。最理想的情况当然是每个圆盘落有一个特征值;上面定理中 B 是对角阵,类似于左行右列的相似变换,即变换后有相同的特征值。变化的过程就相当于改变圆盘的半径,让他们互不相交,达到理想的情况。
幂法
本质上是一种迭代方法。
A 的 n 个特征值,λ1>λ2 >=…λn
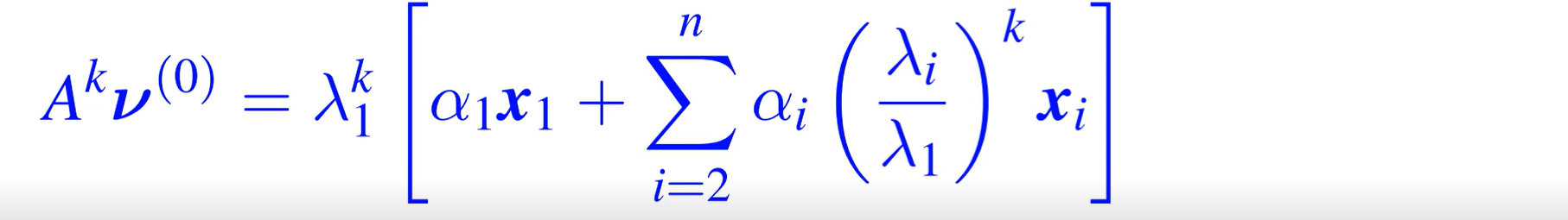
特征值-特征向量定义,当 k->∞,后面一项趋于零;但是前面的极限就一定存在吗?不一定的,无穷-0-or 1 。所以需要做一个归一化,让范数=1。归一化的时候取一个向量的最大值,即无穷范数
幂迭代其实是求 λ1 的方法,主特征值;还能求主特征向量
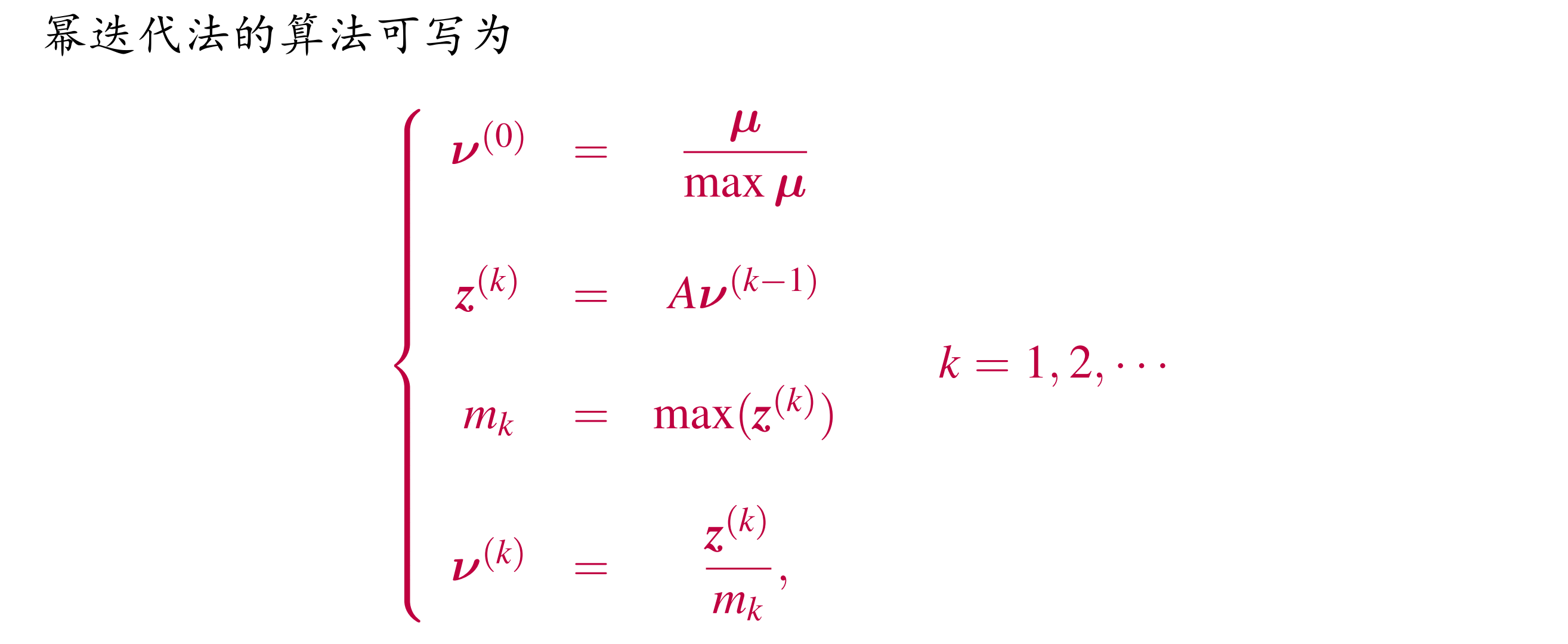
迭代方式:不断地左乘 A,然后归一化。
收敛性:mk 收敛于 λ1,vk 收敛于 xk 的归一化向量;收敛速度是线性收敛,收敛速度取决于 λ1/λ2
逆幂迭代法
主要的思路就是求 A 逆的特征值,体现在迭代步骤中就是第二步 zk=Avk-1 变成 Azk=vk-1。这样求出 A 逆的主特征值,相当于 A 的最小特征值。
得到最大最小的特征值,则可以通过原点位移技巧来求中间的特征值,要求是中间特征值和其他特征值严格分离。
假设中间特征值和数值 q 最接近,则矩阵(A-qI)^-1 的主特征值为 1/(λi-q) 。也就是求(A-qI^-1 的幂迭代。mk 会收敛到 1/(λi-q)。确定 q 就是在确定圆盘,通过近似特征向量来确定。
幂法的优势是足够简单,循环迭代归一取极限,但是迭代多次才得到一个特征值,速度太慢了。总得有些一次性求出 n 个特征值的方法,QR 迭代。
householder 变换
作 QR 分解的一种工具

w 定义了之后的 householder 变换,P u 相当于 u 与 w 垂直的平面镜像,初等反射。
性质:

正交对称;正交变换不改变二范数;利用第五个性质可以构造 w
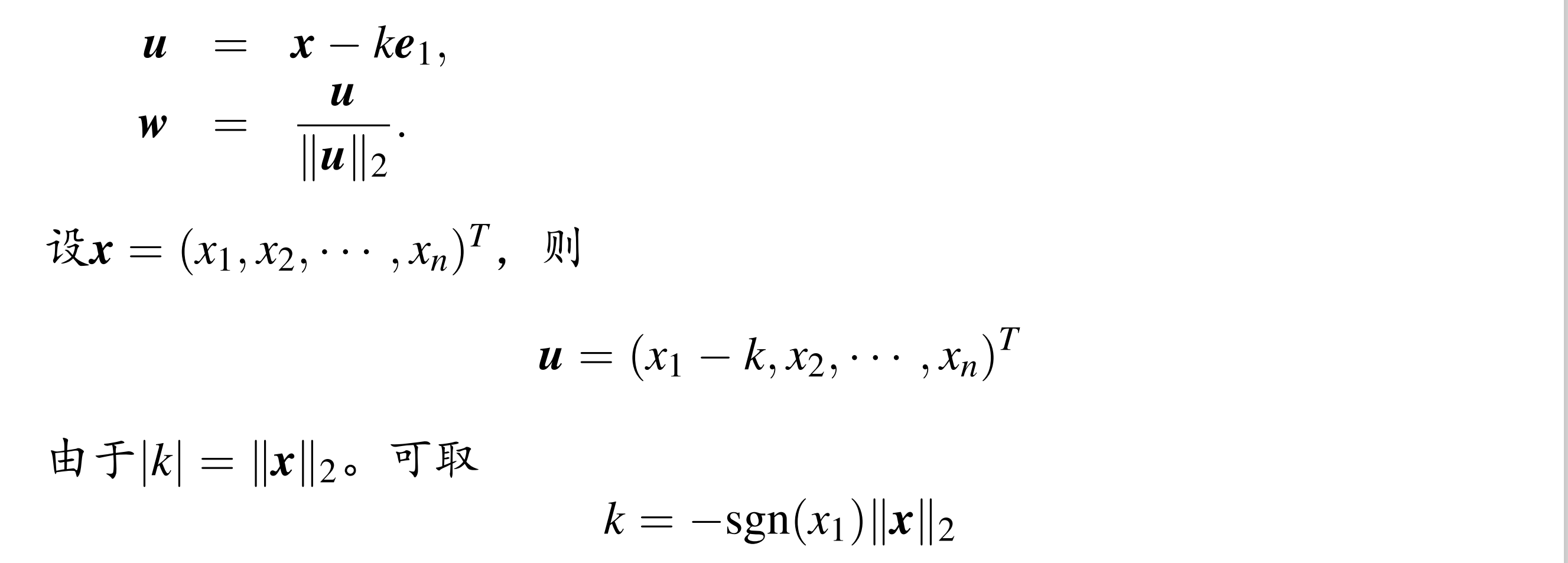
e1 是只有第一个分离的方向向量,需要使 ke1 的二范数等于 x 的二范数,同时符号与 x1||x||2 相反(为了避免相近数相减)
W P=I-2wwT,Px=ke1
上面构造的变换使得 x 变换后除了 x_1 都为零;类似的,可以构造使得 j+1~k 变换后为 0 的 P;子矩阵-
此时 u 的 j~k 分离不为 0:
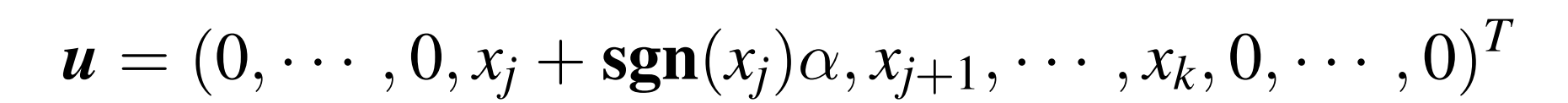
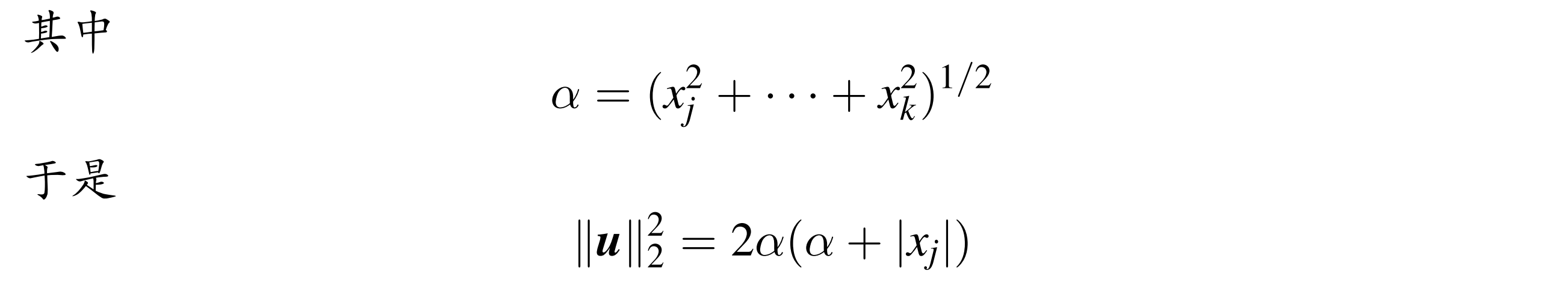
w=u/||u||2 变换后的 Px:
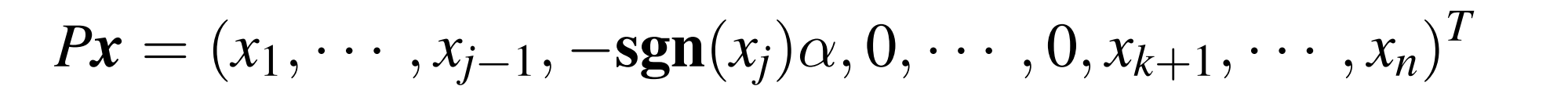
就像是从原来的 x 中取中间一截置 0.对应的变换矩阵,除了中间一截都是单位阵形式。中间的部分 P‘,类似于之前的整个变换。
givens 变换,在二维是一个旋转变换矩阵:
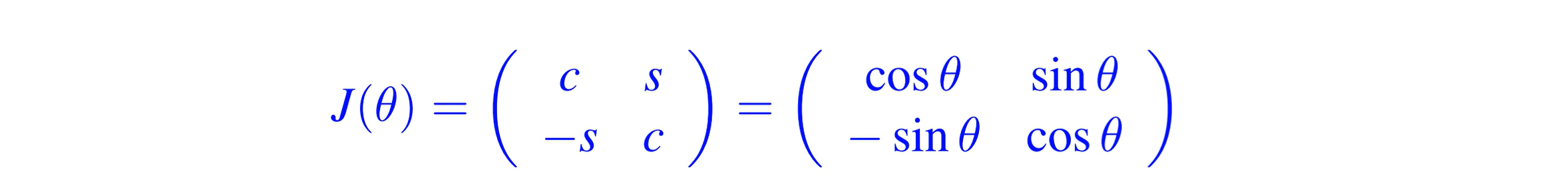
Jx 等价于将 x 顺时针旋转 θ 角
推广到 n 维的情况,J(i,k,θ)相当于变换 i j 两行,左乘 J

具体的计算过程很像三角函数的公式。x,y,sqrt(x2+y2)
QR 分解
一次性求出 n 个特征值的方法,QR 迭代。A1=A;AK=QKRK;AK+1=RKQK

ATA=RTQTQR=RTR,可以看成是 ATA 的 cholesky 分解。
用 householder 变换或 givens 变化把 P2P1R 变成上三角矩阵,然后 Q=P2P1 T。R 对角线元素有非正,则中间分别左右乘对角阵 D。
变换好难啊-注意 householder 和 givens 的变换矩阵 P 都是正交阵,所以 Q 也是正交。
谱分解定理:
AX=XD < ==> Axi=λixi ,只是 X 是 xi 特征向量组合成的矩阵,D 是 λi 对角阵 ;看上去很合理啊,
QR 迭代,希望迭代到一个对角阵。迭代的过程是在不断的相似变换。

H-共轭转置,是正交矩阵 QQT=I 的推广;承酉矩阵相当于酉相似变换
雷姆了,第一次见到酉矩阵的用处。Schur 分解和 QR 分解很像,有一个很好的性质:
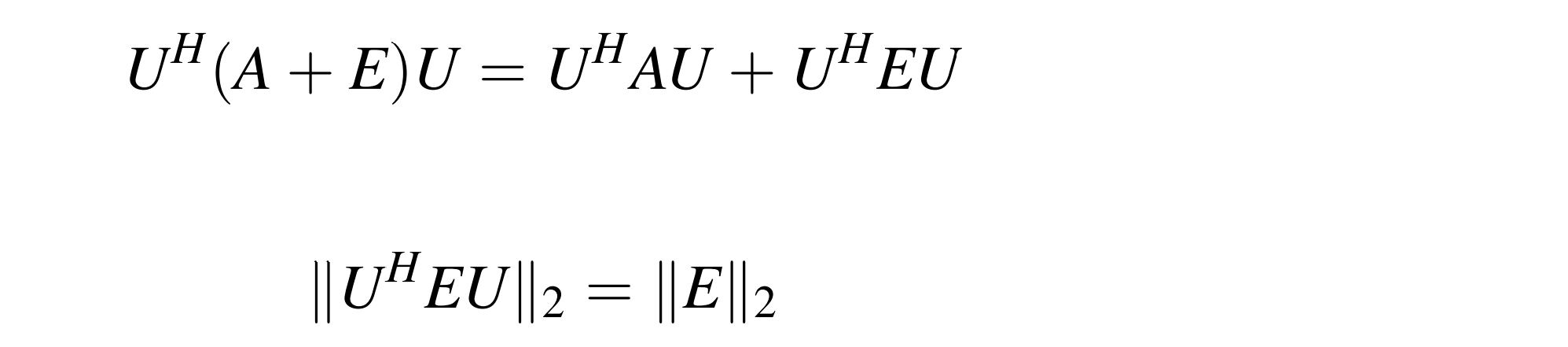
不放大误差;但是注意共轭是在复数域,所以计算 U 会很复杂。
Schur 分解:

类似于上三角矩阵分解,注意正交阵变换不改变特征值,所以对角元素就是特征值。QR 迭代的目标就是得到最后的上三角形式。
A1=A;AK=QKRK;AK+1=RKQK ==>R=Q^TA=A(K+1)Q^T ==> Q^TAQ=A(K+1)
hessenberg 矩阵:

这个就是 schur 分解的形式很相似,但是约束更弱。
变换过程:使用 householder 变换,对于第 j 列,a1jajj 不变,但是 aj+1janj 变为 0
注意左乘完 householder 变换阵 Pi 再右乘一个 Pi,作相似变换-不改变特征值;变成 hessenberg 矩阵而不是直接变成上三角阵,是因为在 hsh 变换的时候,如果按着上三角阵变,中间会把之前的 0 变回去。
n-2 次 hsh 相似变换就可以把 A 变成上 hessenberg 矩阵;注意,正交相似变换保证对称性,所以若 A 是对称阵,则变换完的矩阵是三对角阵。
QR 迭代

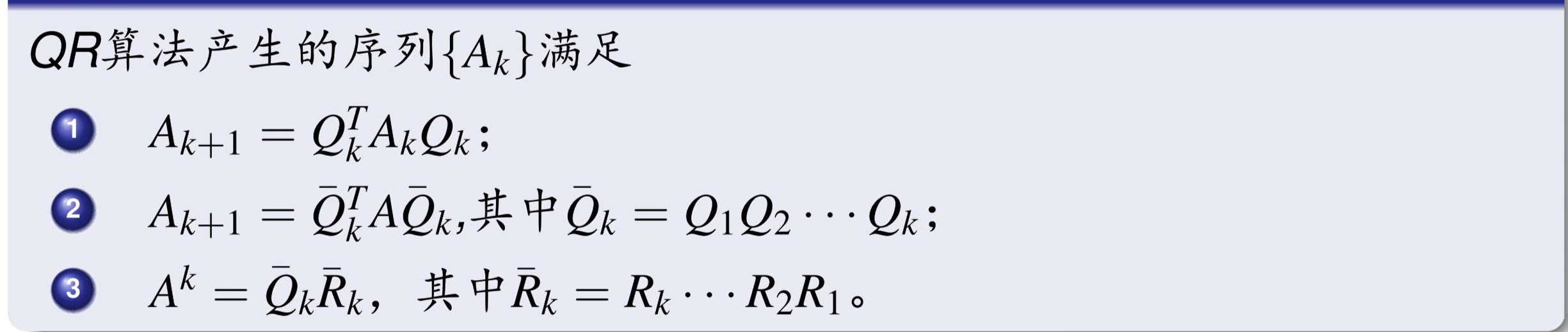
每次迭代都要错一次 QR 分解。
就讲到这了,晦气 差最后一步不讲完害我白复习那么久

迭代求解的思路