【课程学习】信号分析处理
测试信号分析与处理课程笔记
WEEK3 DFS
一些简单的性质:线性、奇偶虚实 - 实信号 频域幅值偶对称相位奇对称
对于一个 δ 信号,频谱是一个 A=1 横线 ;直流信号的频谱是 2pi δ
时域乘 exp(jωt) 频域频移 -ω ;时移 to 频 AXexp(jωto) 相位变化
时域拉伸 频域 f 变窄 ,同时幅值 a 压缩
时域卷积 等于 频域相乘
相关: 频谱 X*Y
离散信号的频谱是周期函数 DTFT Discrete-time Fourier Transform
所有有限长的信号 可以看作无限长加矩形窗 窗会导致频谱出现失真
所以在时域内对信号截断时,窗长会影响频谱分辨率 窗长太短会导致频谱分辨率过低
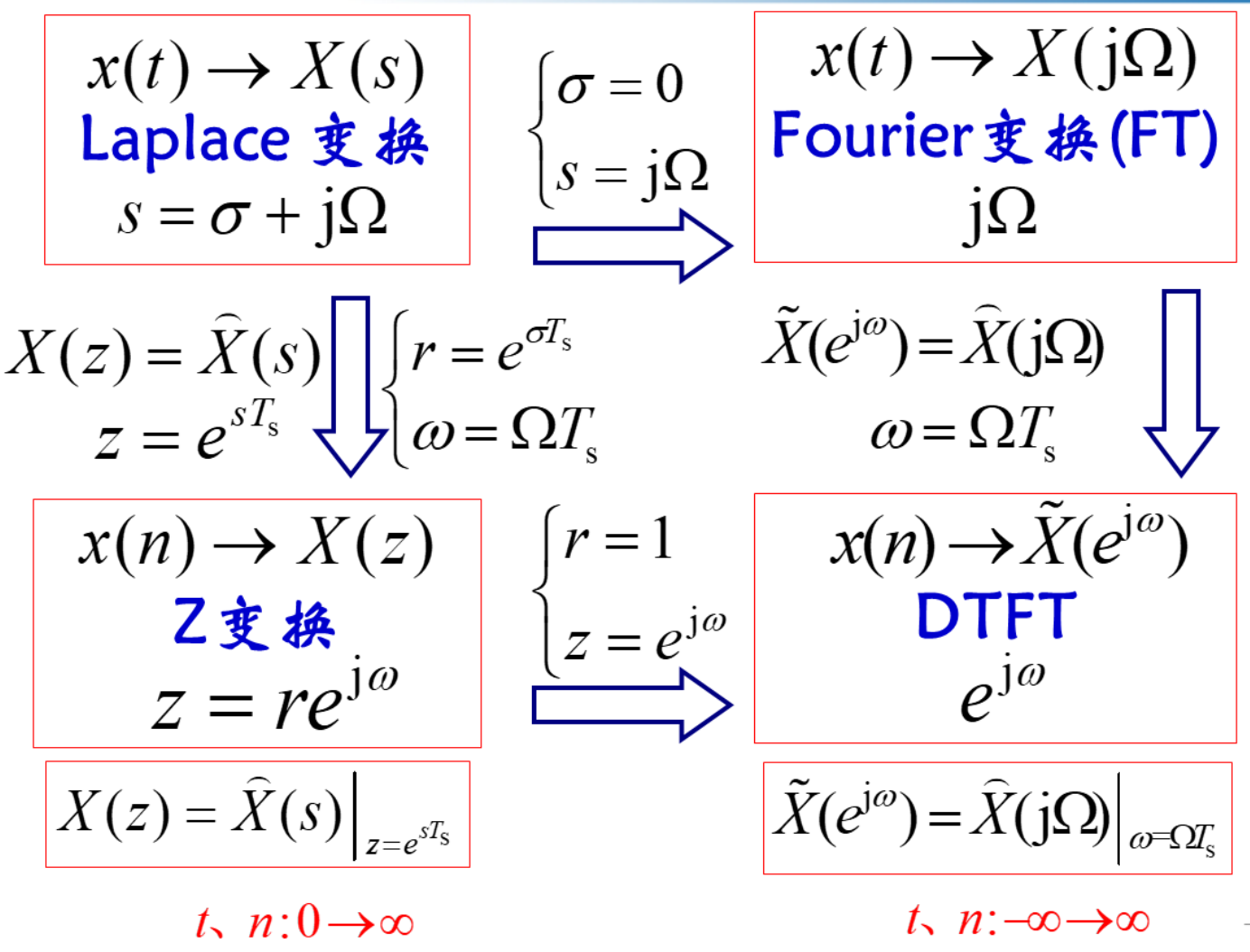

WEEK5 DFT
FS 连续周期信号的傅里叶级数
FT DTFT
DFS 离散周期信号的离散 Fourier
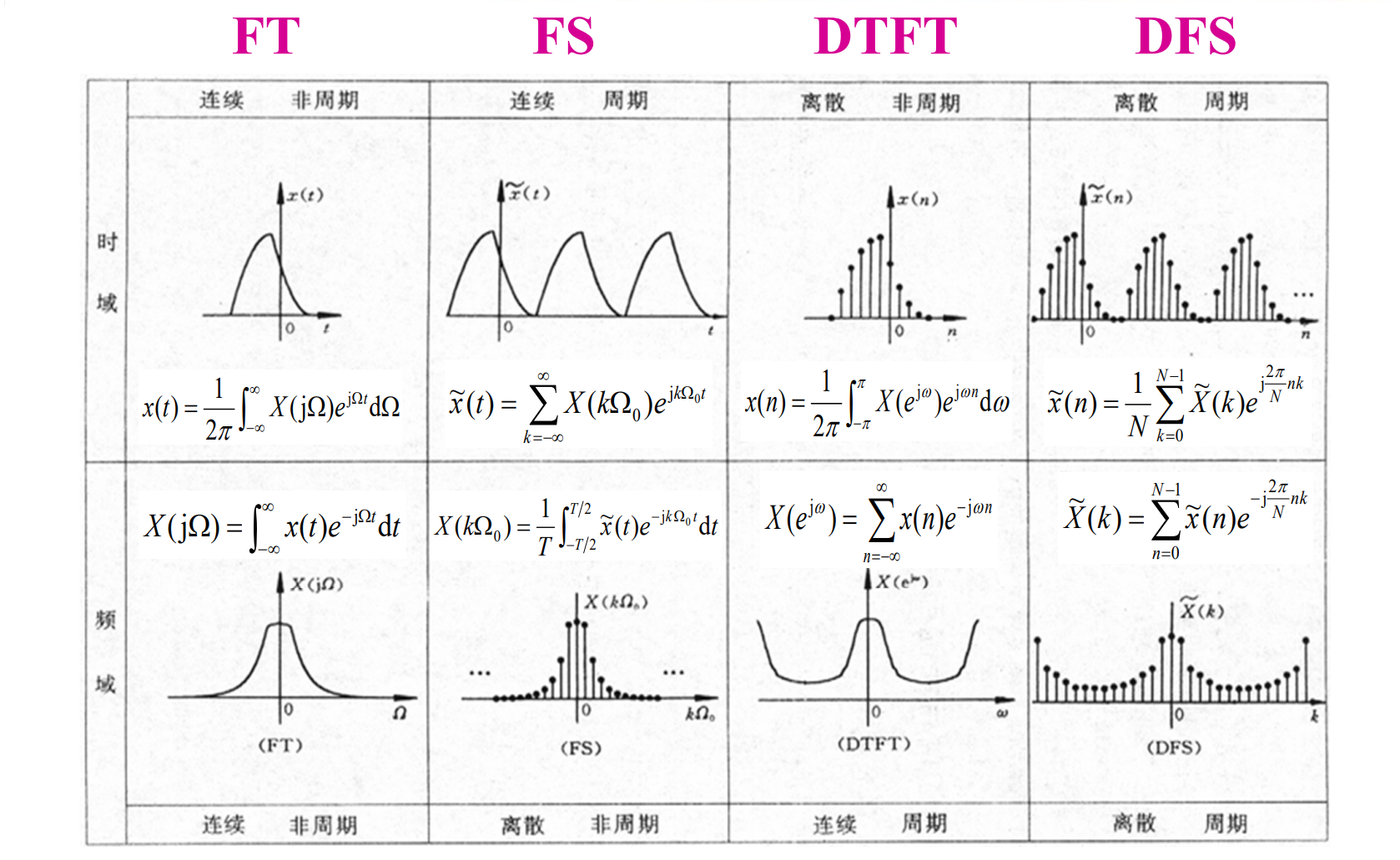
DFT:在做 DFS 时 取一个周期表征信号
DFT 是 DFS 简化的表达;这是表征的周期信号的一个运算。
计算机的数组(时域 or 频域)只有 离散、有限长 计算机的处理结果 需要周期延拓
离散傅里叶变换,实质上是用来表征离散傅里叶级数的。。
工程信号:截取、采样离散化;本质上是采样到一段连续有限长的信号,然后离散、作 DTFT ,然后频域周期延拓并离散化,相当于时域卷积频域采样脉冲。最后就是 DFS 离散周期 -》离散周期。最后再取一个周期,计算机中的 DFT
DFT 后的坐标轴 0~fs 间隔是 fs/N;
实信号 幅值谱关于频率 N/2 偶对称 幅值谱奇对称
移位:相位变化 ; 卷积:循环卷积 离散卷积的矩阵 对角线上也有内容。y(n)=x(n)卷积 h(n)
DFT 对应的是循环卷积;可以通过一定的变换计算线性卷积 ,线性卷积的原序列 x(n) h(m) 都补 0 到 n+m-1 的长度,再作 DFT 频域相乘再 IDFT
DFT 的分辨率?
分辨率和哪些因素有关?仅仅是采样点数 N 和采样频率 fs 吗?需要考虑频率分辨率和时间分辨率。
频谱分析的算法也会影响分辨率。
FT 的频域分辨率,由截断长度决定,矩形窗第一个过零点 2pi/T。DTFT 会多出一个采样,2pi/N。主瓣宽度-分辨率,也是由采样点数 N 决定。都是时域长度越长,频域分辨率越高。分辨率不够会导致谱泄露。
对于 DFT,也是由采样频率和采样点数确定。 fs/N<=Δf
当截图的时间长度不变,增加采样点能提高分辨率。-? 有用,但不明显
补 0–?通过补 0 能增加采样点数。但是只能提高计算分辨率,但是实际没啥用。但是当数据过短,可以起到一定的“插值”作用,计算间隔会变密集,减小栅栏效应。看起来更舒服,但本质分辨率不够补 0 也没办法解决的。
此外,补 0 到 2 的整数次幂,有利于 FFT 的计算。
进行 DFT 时,先确定 fs。一般会高于 10fc。
对周期信号进行截取要尽量整周期截取。不能补 0。采样点数最好是 2 的整数次幂。
FFT W=e-j 2pi/N 利用周期性和对称性
WEEK6 随机系统&线性系统
随机信号的某些数学特征值可能是不变的 需要统计特性
平稳随机过程:随机过程的统计特征不随时间变化
平稳随机过程判据:均值与 t 无关,Rxx 与时间起点无关
严格的平稳随机过程:概率密度函数不随采样时刻变化;平稳随机过程的统计特征不依赖于采样时刻
数学特征:均值、均方值、方差、相关函数、协方差;功率谱密度函数
遍历:一定是平稳的随机信号,各态历经,可以用任意一个样本的全部时间历程数学特征描述
概率密度函数 Px 概率分布函数 Fx Px=dFx/dx
均值:m ; m_x=E(X(n))=∫ xp(x,n)dx
均方值: ψ^2_x (t) = E(x(t)^2)
方差: σ^2_x (t) = E((X-u)^2)=ψ^2-u^2
自相关函数:Rxx=E(X(n)X(n+m)) 性质:偶函数,极大值在 0 取得,R(0)=ψ^2 R(∞)=u^2 ;
互相关函数:Rxy=E(X(n)Y(n+m)) 实 平稳信号的互相关:Rxy(τ)=Ryx(-τ)
协方差函数:可以描述两个随机变量的线性独立关系、正交关系及相关系数。
随机信号在频域的特性:

频域 功率谱
线性系统


输入过程与输出过程的互相关函数等 于系统的冲激响应函数与输入过程的 自相关函数之卷积积分
平稳随机信号– 自功率谱密度函数 《=》 自相关函数 傅里叶变换对

预测 辨识 诊断;
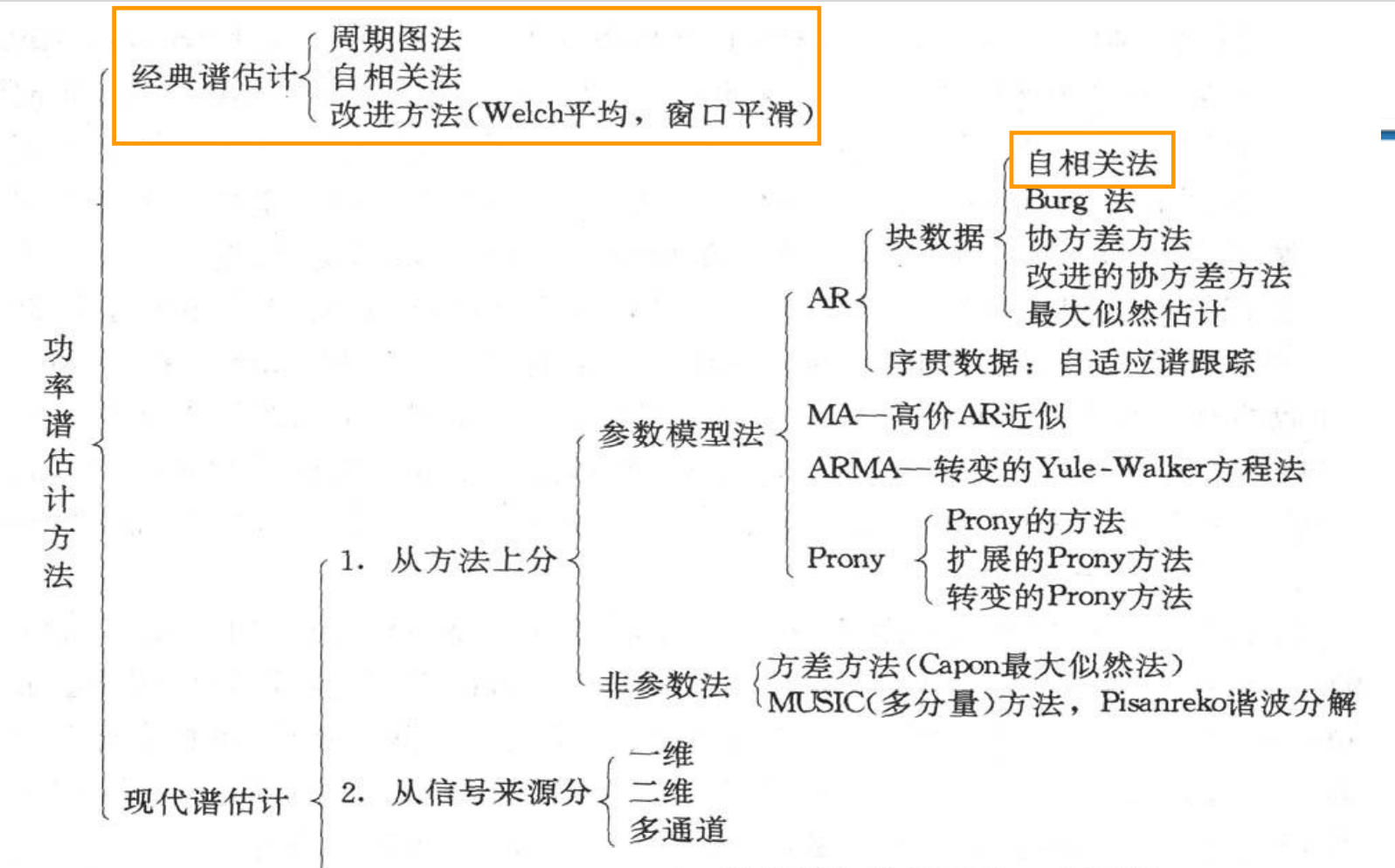
功率谱经典估计法
用数字特征判断平稳;估计-计算方法 ;用偏差和方差进行估计
平稳随机过程-用数字特征表示,与时间起点无关;各态历经–
相关函数的估计:
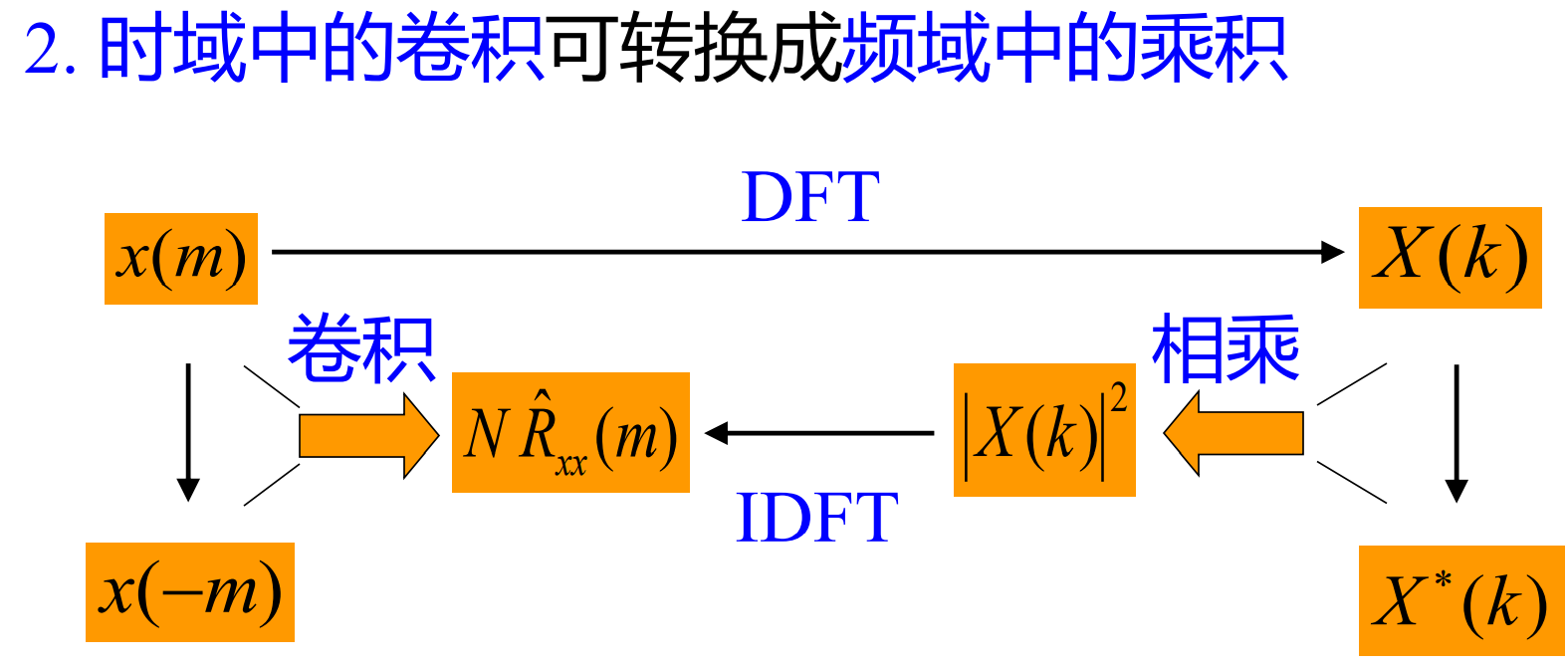
上面这张图展示的是 FFT 作快速自相关估计
注意补 0 – 线性卷积 补到 2n

自相关函数 Rxx 保留同频的周期性
xcorr MATLAB 求相关函数的函数
应用:信号分析
心电信号的检查-自相关函数估计信噪比-人体运动检测-
对信号采样时,理想情况当然是频谱 δ 函数(时域 C),但大多数时候都是 sinc 函数,即时域窗函数采样。
加窗: 实际就是如何安排时间窗内的权值 ; 使信号在窗的边缘为 0 ,以减少由于截取所产生的波形不连续效应 ;我们希望信号经过窗函数加权后,不要丢失太多信息
对平稳随机信号,功率谱密度函数 与 相关函数 互为傅立叶变换对
周期图法 (Periodogram) 直接建立在功 率谱的定义式上。(直接法) ;作 FFT 后求模平方/N
自相关法:功率谱密度函数 与 相关函数 互为傅立叶变换对 ;对信号补 0、求线性卷积、求模平方 ÷N
两种方法原理本质上是相同的。渐进无偏的非一致估计,方差不为 0
自相关函数-时域中的卷积-DFT-频域中的乘积-IDFT-自相关函数
功率谱估计:样本在单位频带内的平均功率
功率谱密度和自相关函数是傅里叶变化对
为什么要估计功率谱?这是一个频域分析的重要方法,做频谱分析的 FFT 要求是能量有限的信号,但很多周期信号往往不是;但大多数信号都是功率有限的,适用情况更广;功率谱有平方环节,能够加大主要信号和干扰的数值差;用偏差和方差评估质量。
谱估计的周期图法
直接法 频谱功率谱定义式
间接法 维纳辛钦公式 求自相关谱再 DFT
改进:
method1:加窗平滑法 :先作自相关估计 Rxx,再选取合适的窗截取 vm,最后作 DFT
偏差会变大,但是会渐进无偏 方差性能有明显提升,是有效估计。方差的减小是以牺牲分辨率为代价的!
方法 2:平均周期图法,K 个独立同分布的随机变量的均值方差,等于单个变量方差的 1/K
长数据 N 分成 K 段,每段 M = N / K,每 段用周期图法求谱 ,然后求平均
独立性不是很好满足;渐进一致估计,改善了方差性能
功率谱,隐含的就是用一组数据遍历,所以分析的数据会有一些震荡。
K↑, M↓, 偏差大, 方差小, 谱曲线平滑;反之,曲线起伏激烈,谱线的尖 峰保留。
几种求功率谱的方法及其改进;主要目的是让谱方差趋于零,有效估计
welch 普估计法:
把 N 个数据分成 N 段,每段相互独立,也可以互相交叠; 再把每段数据乘上窗函数 ,作 IDFT 后求平均
直接计算的谱估计方差不趋于零,无效估计;计算量也比较大,可以用自相关函数变换;基本的出发点是分更多段使方差减小,同时选择窗优化。
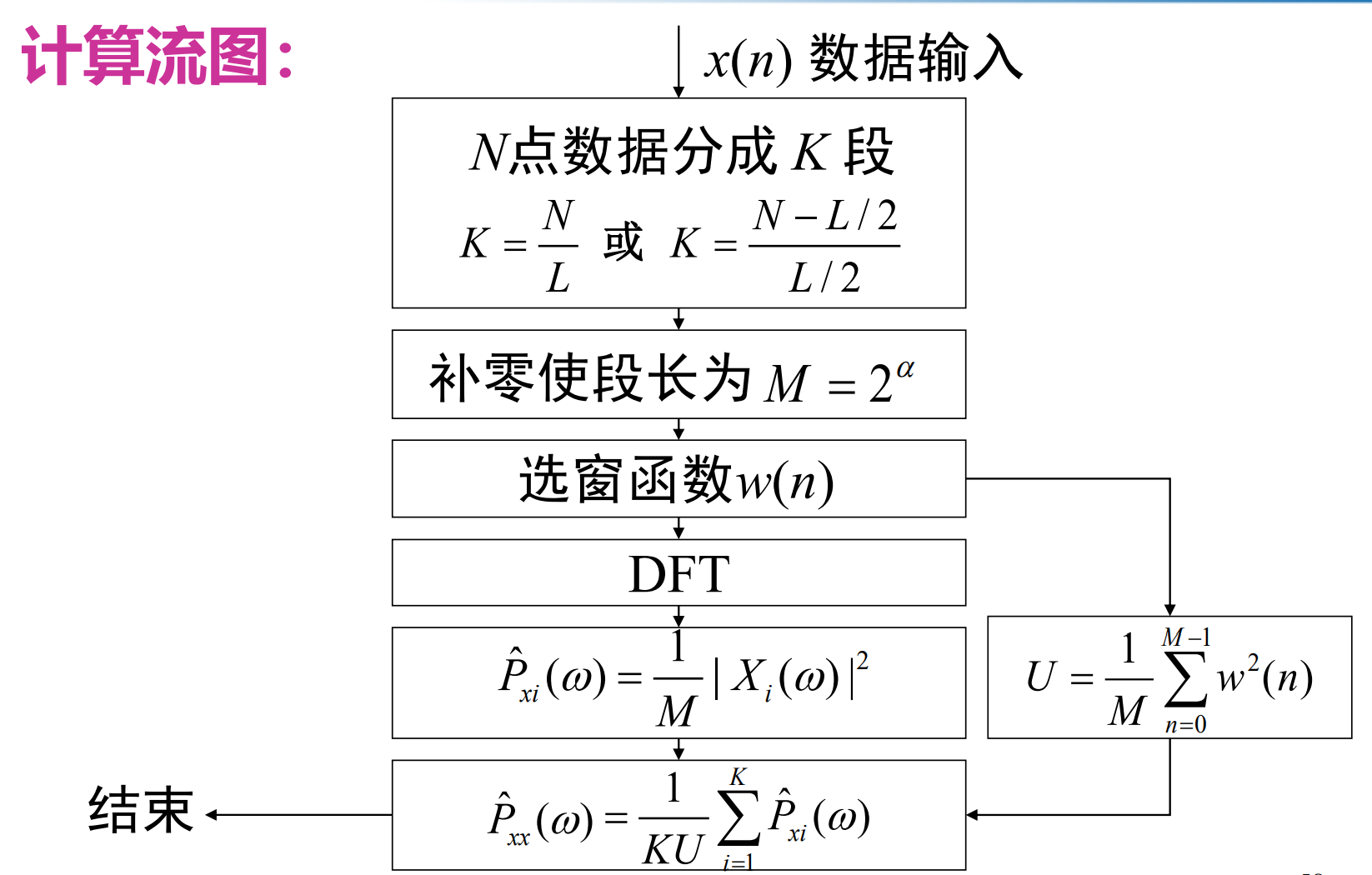
评价:渐近无偏一致估计
周期图法和自相关法等效,渐近无偏非一致估计

现代功率谱估计方法
经典功率谱的估计,方差与分辨率之间存在矛盾。
现代功率谱估计,主要是通过一个系统建模的方法,保证分辨率的同时减小方差
白噪声输入,经过线性系统,由输出得到功率谱
构造线性系统模型;用的最多的是 AR 模型,全极点、
用白噪声 u 激励线性系统产生信号 x,得到线性系统的参数;进而 可以估计功率谱
对应的算法,需要由实际的应用背景,了解算法的数学原理与基本概念
谱分析能干嘛
判断、识别;故障检测;生物电信号解析
仿真实验 1
主要功能:利用 FFT 作相关估计
基本原理:
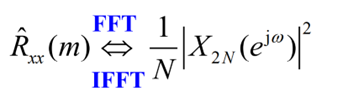
算法步骤:
1.对原序列补 N 个零,得到新序列
2.对 补零后的 X2N 作 FFT 得到 频谱
3,求模后除以 N,得到自相关频谱
4.对 1/N |X2N(k)| 作 IFFT 得到 估计的自相关谱
5.变换位置得到 Rxx
仿真实验 2
滤波器设计
主要是学了滤波器的重要参数,巴特沃夫 切比雪夫 模拟低通滤波器的设计过程;中间需要归一化传递函数;通过一些简单的变换可以把低通滤波器的传递函数转化为高通或者带通滤波器。
在数字滤波器的实现方法上,分为无限冲激响应(IIR)滤波器和有限冲激响应(FIR) 滤波器。这两种滤波器在性能上和设计方法上都存在很大区别
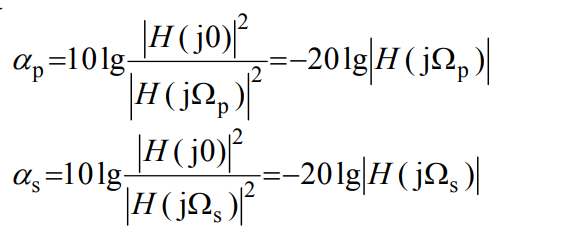
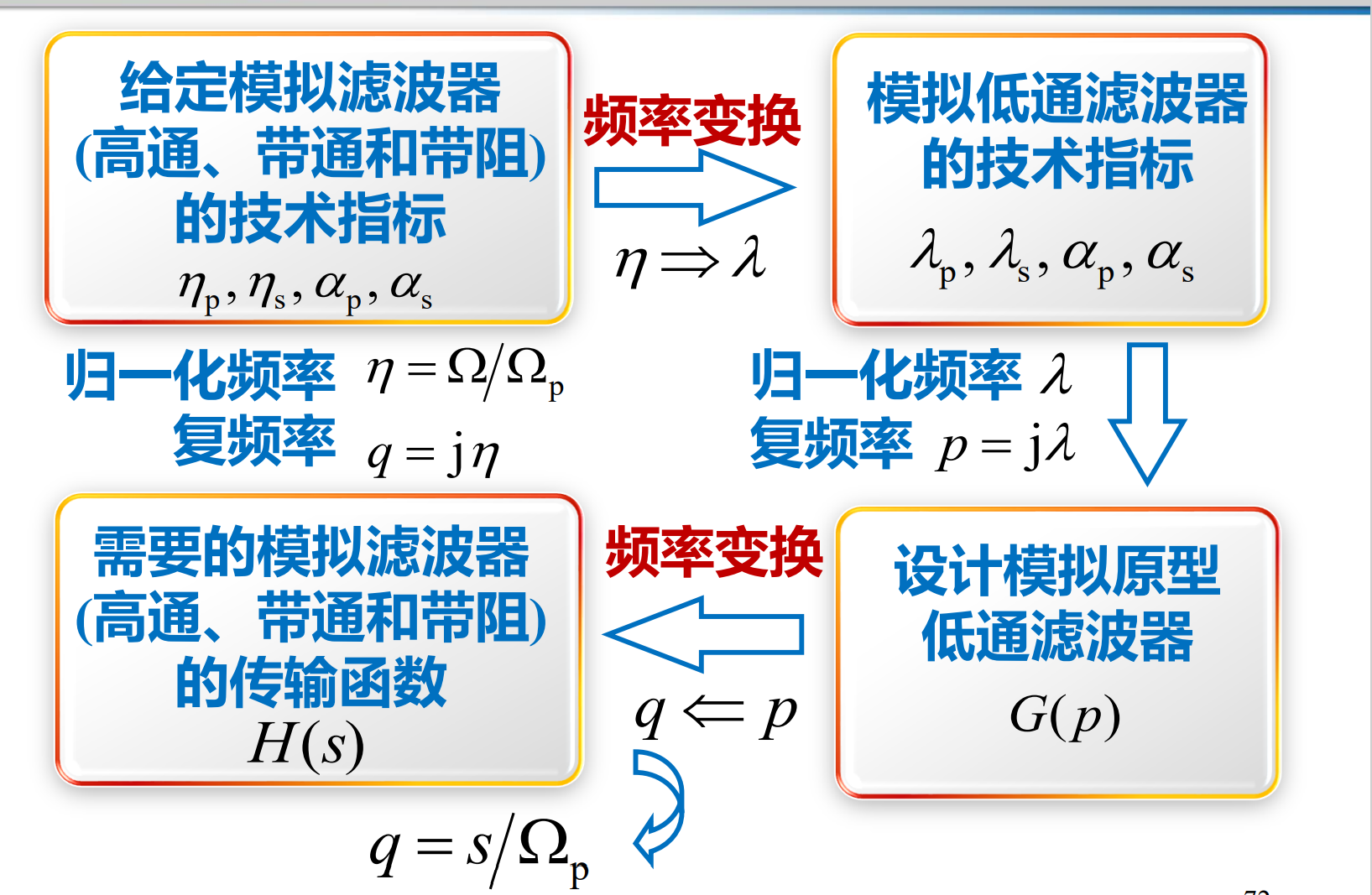
指标参数确定后,模拟滤波器设计的任务就是设法构建一个 传输函数 H s,使其传输特性满足给定的技术指标
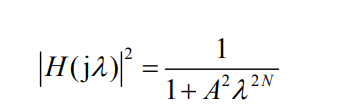
滤波器的设计一般先设计出原型低通滤 波器,再经过频率变换法转换成所需要的其它类型滤波器
一般设计上要求 αp=3dB,代入上式得 A=1

将模拟滤波器变换成数字滤波器,实际上是按照模拟滤波器的设计,在保留满足要求的 模拟频率响应的主要特性前提下,设法得到数字滤波器的系统函数 H z( ) 或冲激响应序列 h n( ) 。或者说,要求把 s 平面上的虚轴映射成 z 平面上的单位圆,为了保证数字滤波器也 是稳定的,若模拟系统只在 s 左半平面有极点,则数字滤波器也必须仅在单位圆内有极点。