【mems】一种三相静电旋转电机的设计
试设计一款静电驱动电机,要求:输出力矩可达 2nNm,驱动电压必须小于 50V。
要求:原理说明、可能的应用背景、结构图、尺寸参数、数学建模(可包含等效电路图、传递函数、仿真等)、工艺流程说明;按照发表的论文的形式(摘要、 关键字、正文、参考文献)
Abstract
静电 MEMS 旋转电机通过转子和定子两极之间的可变电容中储存的电能来运行。本文介绍了一种 MEMS 三相旋转微电机的设计、建模和制备工艺。该电机采用了“蝴蝶形”挠性悬挂枢轴,以避免运行过程中摩擦接触,提供精确、可重复和可靠的双向步进运动。对结构进行了数学建模,在 50V 驱动电压下最大能有 12.285nN·m 的输出力矩和 32° 的行程。结合垂直沟槽隔离和体硅工艺,设计了具有高纵横比电机的微电机制备方法。该电机可以使用在硬盘驱动器中的二级执行器或驱动微泵、微阀或微型镜片等设备。
Keywords:
MEMS,静电力,微电机,三相电机,可变电容,挠性悬挂枢轴,微机械工艺,体硅工艺
Introduction
MEMS 电机的应用范围很广,得益于其小型化、低功耗、高精度的特性,从推动微型车辆、微型机器人到驱动微泵、微阀或微型镜片等设备都有相应的应用。目前大功率 MEMS 电机大多是基于传统电机的电磁感应原理,使用体硅工艺制成的磁感应线圈和永磁体驱动转子旋转[1][2],但是其工艺复杂,成本较高,与平面微加工工艺兼容性较差。目前 MEMS 电机研究的主要方向是静电力驱动型。静电驱动的主要来源是电容器的电场,它依赖于两个带相反电荷的平行板之间的吸引力。它们具有设计简单、响应速度快、易于制造和低能耗的特点[3]。从一个简化的角度来看,梳状驱动器只是由一个带有移动电极的可变电容器组成。然而,静电型电机需要高输入电压,而且它的扭矩一般较低。在一些低速、低功率的应用场合,静电型 MEMS 电机更具有优势。
典型的三相静电旋转步进微电机的布局和工作原理示意图见图 1[4]。该电机由一个转子和一个定子组成,两者都含有大量的疏齿状电极。转子由一个弯曲的枢轴机构悬挂,它会给转子旋转自由度,同时提供一定的机械刚度。在电机运行过程中,转子电极通过挠性悬架进行电气接地(GND),而定子电极以三个不同相的电位交替。
在工作时,每一相的定子电机分为一组。当相位 φi 被激活时,相应的定子电极和相对的转子电极之间的电压差(Ui)产生了一个静电力。由于对称性,作用在转子上的静电力的径向分量会被抵消,切向分量会产生一个全局扭矩。静电扭矩会驱动电机重新调整转子的电极到和激活的定子相对的位置。在常规的设计中,定子电极的间距会设定为转子间距的 4/3 倍。因此,当某一相的电极与转子上的相对电极完全对齐时,另外两相的电极和定子电极有一个错位,这个错位等于转子间距的-1/3 和 1/3。当电压以适当的顺序施加到每一相上时,转子可以按顺时针(如图 1 所示)或逆时针方向上实现阶梯式运动,从而实现电机的双向旋转。
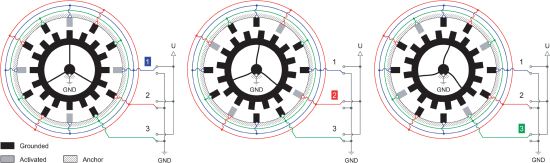
图 1.三相静电旋转步进电机的工作原理。通过在每一相上连续施加电压,实现转子的阶梯式运动。
此外,当以步进模式运行时,这些电机会处于有限数量的稳定状态,稳定状态的数量(分辨率)由转子和定子磁极的空间分布定义。这使得转子的高精度可重复运动不需要复杂的反馈控制,而是取决于设计的定子电极密度和工艺能力。
Design
在 MEMS 电极的转子支撑结构中,一般有挠性结构和摩擦轴承[5]。摩擦轴承能够实现更大的旋转范围、更小的扭转限制,但是触摩擦和由此产生的磨损会影响器件的精确和可靠性。在本次的设计中,使用了挠性结构来悬挂转子。挠性结构很容易和平面工艺兼容,同时转子和定子之间可以避免物理解除。此外,挠性体可以作为一种电气连接,通过它实现转子与 GND 的连接,避免了复杂的布线。最后,挠性体的机械刚度虽然会减小电极的驱动能力,但其恢复力决定了转子在静止时的确定位置,电机的旋转范围也会受到保护。
挠性转子悬架的典型结构如图 2 所示。图 2(a)所示的平行四边形挠性枢轴一般会用在直线型执行器。图 2(b)所示的旋转执行器平行四边形挠性枢轴可以看作是(a)的演化,可以用作旋转执行器的悬挂。图 2(c)的蝴蝶形挠性机构可以看作是四个(b)的串联叠加,它相较于同尺寸的(b)结构,可以提供更大的旋转行程、更小的机械刚度和跟小的旋转中心偏移[6]。
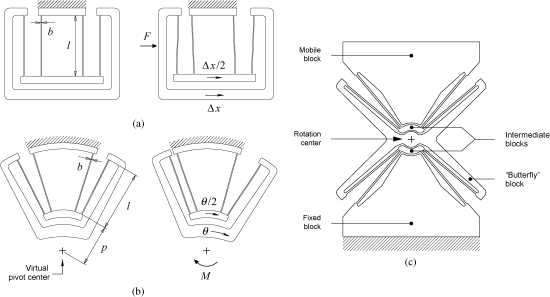
图 2.用于直线和旋转导向的挠性机构。(a) 用于直线引导的“双平行四边形挠性结构”的示意图。(b) 用于旋转导向的 “挠性支点 “示意图。(c) “蝴蝶形”枢轴,由四个串联的基本挠性枢轴组成。
蝴蝶形挠性枢轴在 2003 年提出,旨在建立了一个可以通过 IC 工艺加工,可以单体制造,具备非常小的寄生中心平移的结构。这种结构由四个串联的基本枢轴组成,它们的四个旋转中心都在一起,具体的结构见图 3。第一对挠性叶片连接中间块 1 和固定基座,它对于轴线 O 具有一个旋转自由度。第二对挠性叶片连接中间块 2(蝴蝶形结构)和中间块 1。类似的,第三和第四挠性叶片用于连接中间块 2、3 和旋转移动块。由于所有的挠性叶片都是相同的,所以基本枢轴的旋转刚度都是相同的。因此,当对移动块施加一个角度 α 时,四个枢轴平均分担行程(即块 2 相对于固定块旋转 α/4,块 3 旋转 α/2,块 3 旋转 3α/4),系统的整体旋转刚度为单个枢轴的四分之一。
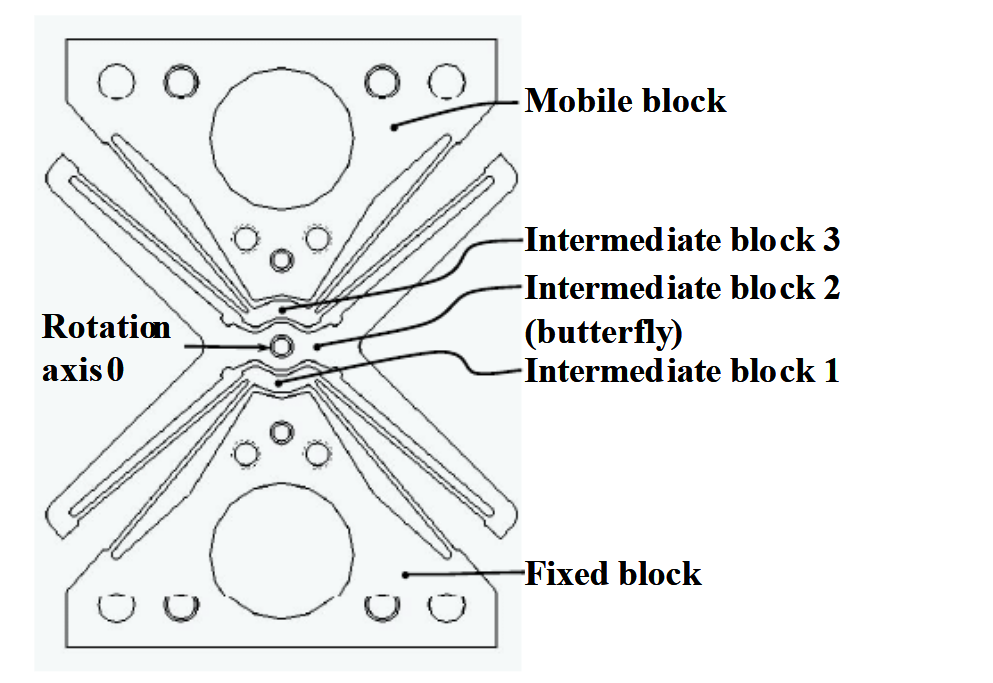
图 3.”蝴蝶形”枢轴结构示意图。通过四个基本挠性铰链串联,使它们各自的寄生偏移矢量有效地互相补偿,从而减小中心偏移。
考虑图 2(b)中的挠性枢轴,当我们施加一个切向的旋转驱动力时,由于挠性梁长度方向不易变化,可动部分的旋转中心和所设计的选中中心会有一定的偏移,我们把这个偏移量称作寄生偏移矢量。而”蝴蝶形“枢轴通过将四个基本挠性铰链串联起来,由于这些偏移矢量的方向和大小不同,它们会产生一个合成矢量,其方向和大小是所有偏移矢量的矢量和。基本挠性铰链串联时,寄生偏移矢量会相互作用,它们的排列方式使它们各自的寄生偏移矢量有效地互相补偿。因此,”蝴蝶形“结构可以补偿中心偏移。
在本文的设计中,考虑到实际转动情况,将”蝴蝶形“与转子结合,作为旋转件;两个连接块作为固定件。在 3D 建模软件中构建 MEMS 电机的基本结构,在此我提供了所建模的模型,见下方附件和图 4。
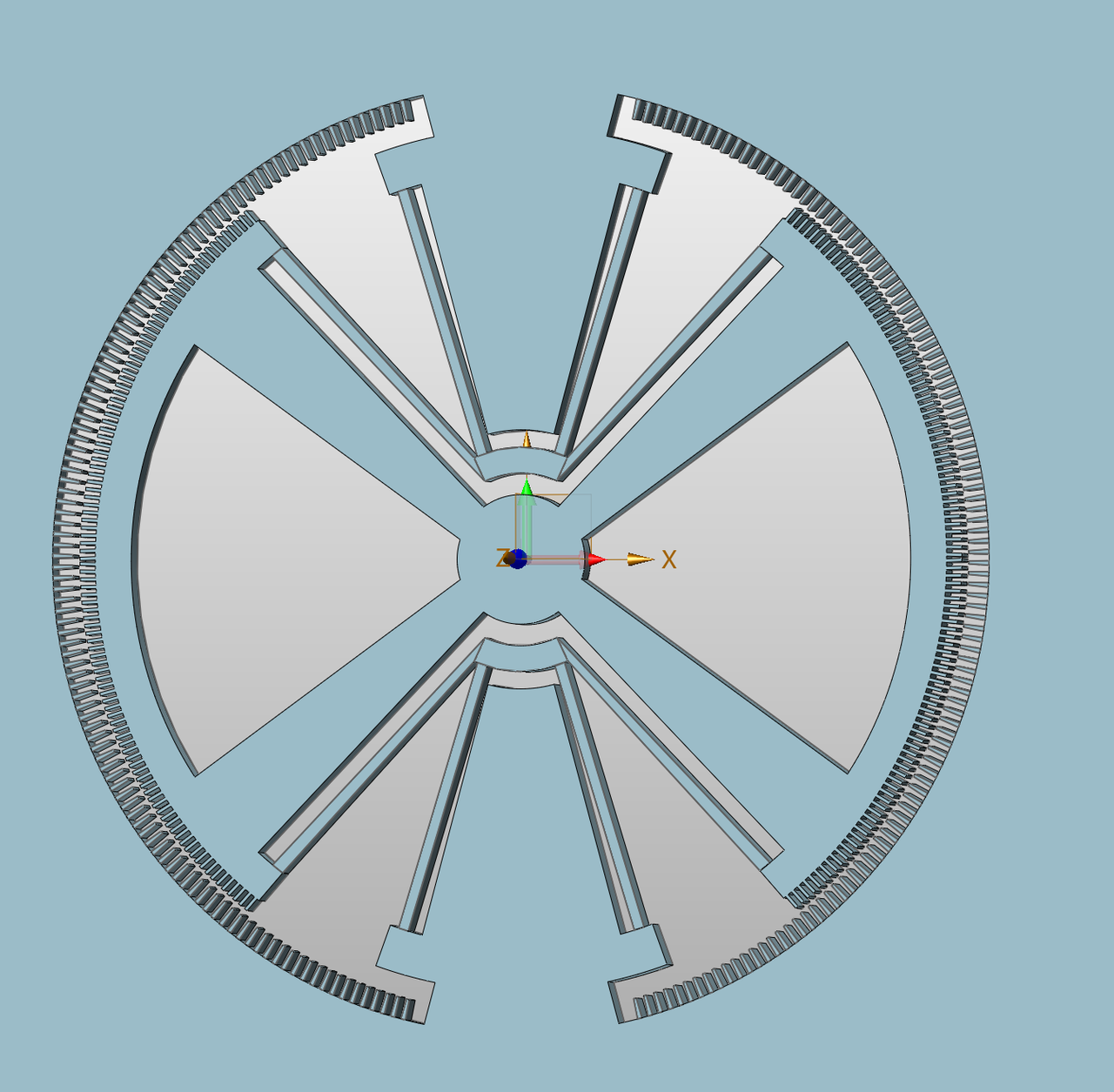

在所设计的结构中,上下两个固定块通过绕行枢轴和转子”蝴蝶“连接。由于每个枢轴平均分担行程为转子总行程的二分之一,所以整体旋转刚度为单个枢轴的一半。在设计定子电极和转子电极的间距时,需要考虑电机的驱动能力、行程和工艺尺寸分辨率:电机的特征尺寸越小,每一相电机数越多,驱动能力越大,同时增大”蝴蝶枢轴“的弧度也能增多转子电极数,但会因为机械干涉减小器件的行程。所以,在初步设计中,转子间距为 1°,数量被设计为 204 个,不考虑驱动能力的最大行程为 ±16°。完成大致结构设计后,需要进行具体的尺寸参数和结构参数设计,具体参数的含义与设计结构见下节。
Molding
在本节中,将对所设计的 MEMS 电机进行静态建模。首先会计算三相静电驱动所产生的扭矩。然后,通过悬架的机械刚度将静电扭矩与转子的角位移联系起来,最后进行了尺寸参数的设计。
转子的旋转位移 θ 与静电扭矩 M 成正比,与蝶形悬架的刚度 Kθ 成反比。该扭矩是由作用在转子和定子两极之间的静电力的切向分量产生的。施加在单个转子极 j 上的切向力 F 可以用平行板电容公式来估计。通过可动平行平板电容存储的能量对宽度方向的偏微分,可以得到单个电极对的切向静电力:
$$
F = \frac{\varepsilon LU^{2}}{2g}\tag{1}
$$
其中 L 是电极的高度,g 是转子和定子电极之间的间隙,ε 是空气的介电常数,U 是施加在相关相上的电压。需要注意的是,(1)不包括边缘效应,因此是一个粗糙的近似值。
从(1)中,我们可以推导出由相位 φi 施加在转子上的静电扭矩 M:
$$
M = \frac{n \varepsilon LU^{2}r}{2g}\tag{2}
$$
其中 r 是转子半径。由于 g<<r,所以上式简化了 g 的影响,n 是一相中的电极数。
我们所使用挠度枢轴会有弹力限制旋转,接下来计算挠性梁的旋转弹性系数。单个挠度枢轴的原理图如图 5 所示,枢轴是由两根梁 AB 和 A′B′组成的旋转导向。它的旋转轴线与两根梁在静止位置的交点平面所定义的线大致吻合,当挠度枢轴受到以 C 为中心的弯矩 C(↶)时,每根梁都会承受以 C 为中心的弯矩 M0=C/2。因此,对该机构的刚度计算可以通过应用于单根悬臂梁的计算实现。
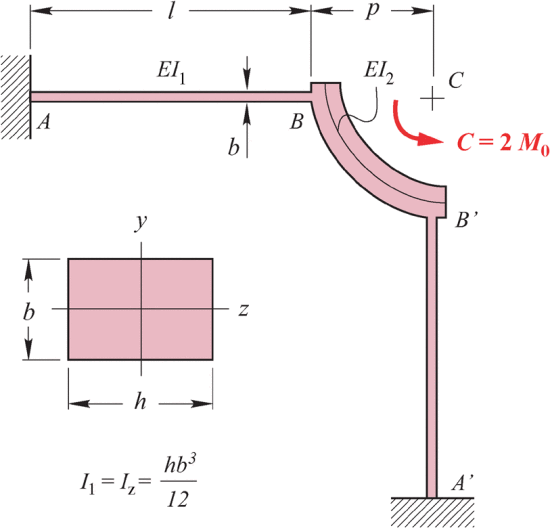
图 5.单个挠度支撑梁的示意图
关于单个挠性结构的旋转刚度可以见文献[4]的附录 A。在此简要说明计算步骤:
- 设一个梁的两个端点为 A 和 B,它们之间的距离为 l,枢轴的宽度为 b,厚度为 h。
- 根据弯曲应力公式,计算梁上任意一点 P 处的应力 σ,其中 P 距离 A 的长度为 x,距离梁中心线的高度为 y。
- 根据应力和应变之间的关系,计算枢轴上任意一点 P 处的应变 ε。
- 根据应变和位移之间的关系,计算枢轴上任意一点 P 处的位移 u 和 v,其中 u 是沿着 x 方向的位移,v 是沿着 y 方向的位移。
- 根据位移和角度之间的关系,计算枢轴上任意一点 P 处的角度 θ。
- 根据角度和扭矩之间的关系,计算枢轴上任意一点 P 处的扭矩 M。
- 根据扭矩和旋转弹性刚度之间的关系,计算枢轴的旋转弹性刚度 Kθ。
所对应结构的旋转刚度:
$$
K_{\theta} = \frac{M}{\theta} = \frac{4EI}{l}\left(1 + 3\frac{p}{l} + 3\frac{p^{2}}{l^{2}} \right),\qquad \text{for}\ \sin\theta \approx \theta\tag{3}
$$
其中 E 是梁材料的杨氏模量,l 是梁的长度,I 是其中心惯性矩,p 是悬臂梁端点到虚拟旋转中心的距离。对于矩形截面的梁,惯性面积矩是平面外高度 h 和宽度 b 的一个函数:
$$
I = \frac{hb^{3}}{12} \tag{4}
$$
对于所设计的蝴蝶型挠度支架,弹性系数为单个挠度支架的一半
$$
K_{\theta\vert \otimes} = \frac{K_{\theta}}{2}\tag{5}
$$
考虑性能要求和应用场景,设计如下尺寸参数:
表 1.尺寸参数设计
计算驱动力矩和旋转刚度时,保守估计,选择 <1,1,1> 晶相的单晶硅,杨氏模量为 188.5 GPa。空气的介电常数为 8.854e-12,在 U=50V 的条件下,计算得到电机的驱动力矩:
$$
M = 1.2285 ×10^{-8}Nm =12.285nNm
$$
挠性枢轴的旋转刚度:
$$
I = 8.3250×10^{-23}
$$
$$
K_{\theta\vert\otimes } = 6.0809 × 10^{-11} N/rad = 0.06nN/rad
$$
设计的理论指标可以满足要求,枢轴旋转刚度对电电机驱动能力的影响较小,能够完成设计的行程。需要注意的是,设计时的数学建模都是简化模型,实际的驱动能力还需要实验测量。本章计算没有考虑梁的最大弯曲应变,但参考文献[4]中基于材料屈服应变计算得到最大弯曲角度有较多冗余。
接下来,将构建静电力驱动型电机的等效电路模型可变电容等效模型。将机械部分(包括转子和定子)建模为旋转系统,可以使用旋转惯量 J,机械阻尼 B 和和旋转刚度 Kθ 来描述旋转系统的动态行为。在转动机械系统中,力矩定义为广义电压,角速度定义为广义电流,转动惯量定义为广义电感,旋转刚度定义为广义电容。电力部分包括了静电力驱动和旋转电机所消耗的功率等,得到的等效电路模型如图 6 所示。
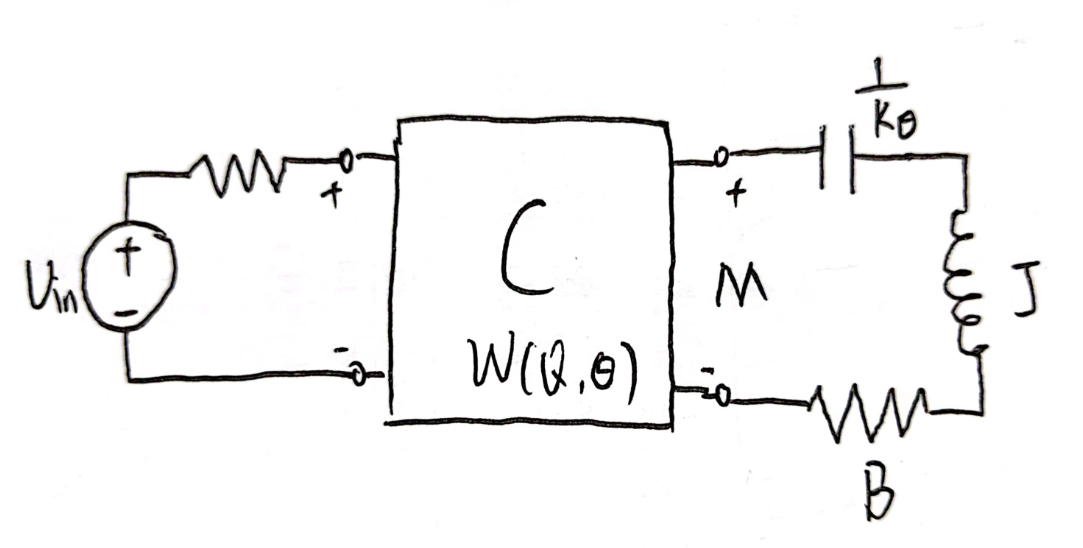
图 6.所设计系统的等效电路模型
对于静电力驱动,参考式(2),可以得到:
$$
\frac{n \varepsilon LU^{2}r}{2g} = J \ddot{\theta}+B\dot{\theta}+K_{\theta}\theta \tag{6}
$$
至此,我们给出了所设计的基于可变电容原理的静电电机由电压驱动转子旋转的模型。
Fabrication
在本节中,我们将讨论所设计结构的具体加工步骤。得益于选择枢轴的平面单体制造特性,我们可以在一次光刻-刻蚀中加工出如图(4)所示的平面结构。但是在加工具体定子-转子结构之前,我们还需要考虑有序分布的三相电极如何加工,以及如何得到足够高度的平面结构。由式(2)可以看到,静电电机的驱动能力和切向的电容宽度无关,而和电机高度 L 成正比。为了获得尽可能大的驱动力矩,我们希望制造具有高纵横比的电极。使用成膜的方法制造高纵横比电极是比较困难的,一般的做法是使用掺杂的硅基体作为电极的材料,通过刻蚀形成电极图案。
在有序分布的三相电极制备中,可以使用垂直沟槽隔离技术[7]。该技术是一种用于制造微电子器件的工艺技术,可以在单晶硅晶片上创建具有高纵横比极和集成电气网络的单片式步进电机。该技术基于 SOI、表面或体积微加工,利用填充有绝缘材料的沟槽来在单个器件层中创建机械连接组件之间的电气隔离。它可以实现高纵横比单晶硅元件的制造,并与集成的三相电气网络结合使用。
图 7 显示了垂直沟槽隔离工艺下定子的布局,并说明了绝缘沟是如何与导线结合以获得三相电网络所需的三级交叉连接的。我们把硅体作为一个大的导体,然后插入一系列垂直沟槽把它们分为 3n 个独立的电极。下一步,通过三个带有导体通孔的绝缘体带附着在分离电极的表面,并循环布置通孔作为电极连接。如图 7(a)中所示,每个定子电极(白色部分)都被绝缘沟槽(灰色部分)所包围,因此它与主体和其他磁极之间是电气绝缘的。在电绝缘的同时,每个电极仍然嵌入在硅体中,因此机械完整性得到了保留。为了将定子磁极连接到其中一个相位,采用了一种导电互连,通过蚀刻在电介质层上的通孔进入磁极。
图 7. 使用垂直沟槽隔离技术在硅片制作定子电极的示意图。(a)定子的顶部和(b)横截面显示了垂直沟槽隔离和互连的布局。(c)是加工出的定子结构的扫描电镜图。
在材料的选择中,互联层和沟槽填充层使用是多晶硅,绝缘层使用的是氧化硅。整体的工艺流程如图 8 所示,在之后我们会详细介绍从(a)到(h)的详细步骤。
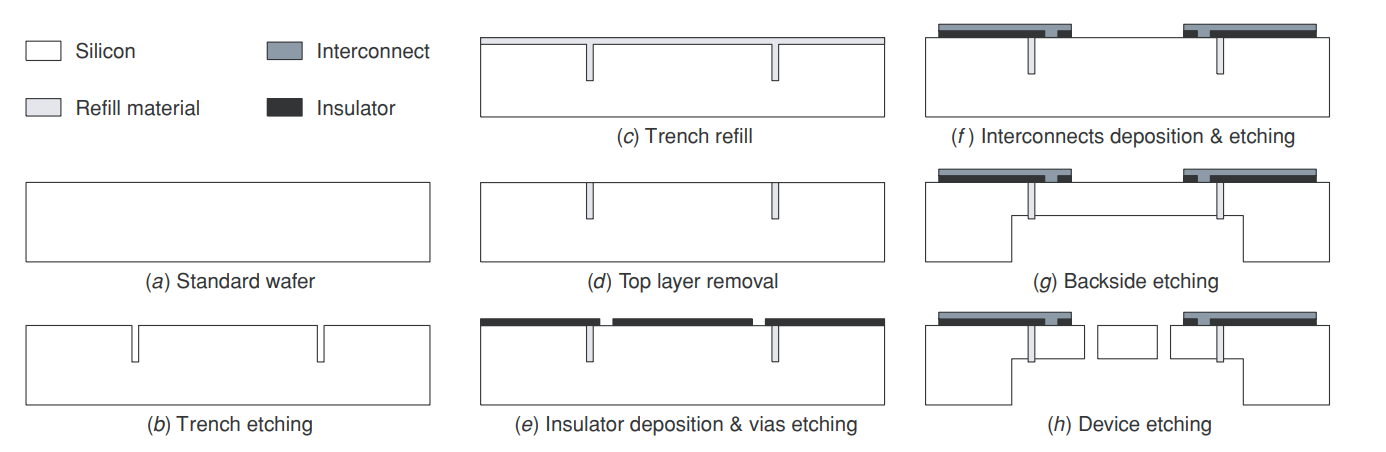
图 7. 使用垂直沟槽隔离技术在硅片制作定子电极的示意图。(a)定子的顶部和(b)横截面显示了垂直沟槽隔离和互连的布局。(c)是加工出的定子结构的扫描电镜图。
- A 备片,清洗,掺杂
在一个 200 微米厚的标准硅片上进行加工,首先进行清洗。随后进行了掺杂,使用磷富含的旋涂玻璃(SOG)对多晶硅层进行掺杂,这种掺杂方法被称为“磷摻杂”,它可以增加多晶硅层的导电性能。
- B 垂直沟槽刻蚀 ,光刻(1#)
在这一步,我们使用显示沟槽的掩模版,进行。通过深反应离子蚀刻(Deep Reactive Ion Etching,DRIE)来蚀刻垂直沟槽。DRIE 是一种高精度、高效率的微纳加工技术,可以用于制造微电子器件中的沟槽、孔洞等结构,该技术利用高能离子束和化学反应来实现对硅晶片的刻蚀,具有刻蚀速率快、精度高等优点。完成刻蚀后除胶。
- C 沟槽填充
沟槽的宽度为 2μm,深 40μm(和电极的高度相同)。通过低压化学气相沉积(LPCVD)将多晶硅完全重新填充氧化硅和未掺杂多晶硅的组合。
- D 沟槽顶层剥离
分别通过 TMAH 和氢氟酸和氢氧化铵混合物(Buffered Hydrofluoric Acid,BHF)溶液的湿化学蚀刻从晶片上表面去除多晶硅和氧化硅。BHF 是一种化学蚀刻液,其全称为。它主要用于蚀刻硅和氧化硅等材料。BHF 的优点是可以高效地去除硅和氧化硅,并且不会对其他材料产生太大的影响。
- E 绝缘体沉积和连接孔蚀刻,光刻(2#)
这一步,我们使用显示连接过孔的掩模版,进行涂胶,光刻,刻蚀,除胶。首先在晶圆上通过湿氧化法生长一个 300 纳米厚的氧化硅层,然后进行甩胶、光刻,再使用 BHF 蚀刻法刻蚀电气通孔。
- F 电极层沉积,光刻(3#)
在这一步中使用顶层电极形状的掩模版,制备顶层的电极形状。首先我们通过 LPCVD 沉积一个 1 微米厚的多晶层,并使用 SOG 进行掺杂。然后,甩胶、光刻,通过 ICP-RIE 蚀刻多晶硅,然后用 BHF 蚀刻氧化硅来形成互连。如图 7 所示,顶层的多晶硅电层为被垂直沟槽隔离的硅区域之间提供电连接,实现有规划的三相电极分布。
- G 背部硅刻蚀,光刻(4#)
这一步中我们进行“背掏”工艺,生成可动 MEMS 器件的悬架结构。我们从背部进行 ICP 蚀刻,首先在硅片背面甩胶、光刻,在把需要“悬空”的部分进行刻蚀。在这一步中我们需要严格控制刻蚀的深度,因为留下的部分即为电极的高度。
- H 器件结构刻蚀,光刻(5#)
在最后的制造步骤中,我们根据图 4 所设计的平面微机械绘制相应的掩模版,进行最后的图案转移。甩胶、光刻,通过 DRIE 在硅膜上进行蚀刻。
Discussion
静电驱动型选择电机的旋转速度与驱动信号的频率直接相关,从理论上速度随着循环频率的增加而线性增加。然而,我们从公式(6)中我们可以观察到转子的转动惯量和系统阻尼会阻碍电极的高速转动。步进电机实际的高频失效表现是:在高驱动频率下,以半步进模式运行的电机显示出漏步或卡顿等不正常运行。另一方面,由于方波激励所固有的驱动力矩的突然变化,快速地将转子从一个位置扣到另一个位置,在公式(6)中表现为角加速度和角速度很大,这显然会影响驱动效果。我们可以通过微步进电平的方式来减小这种影响,如图 8 所示,更平滑的电平变化可以减小驱动需要的电压值。
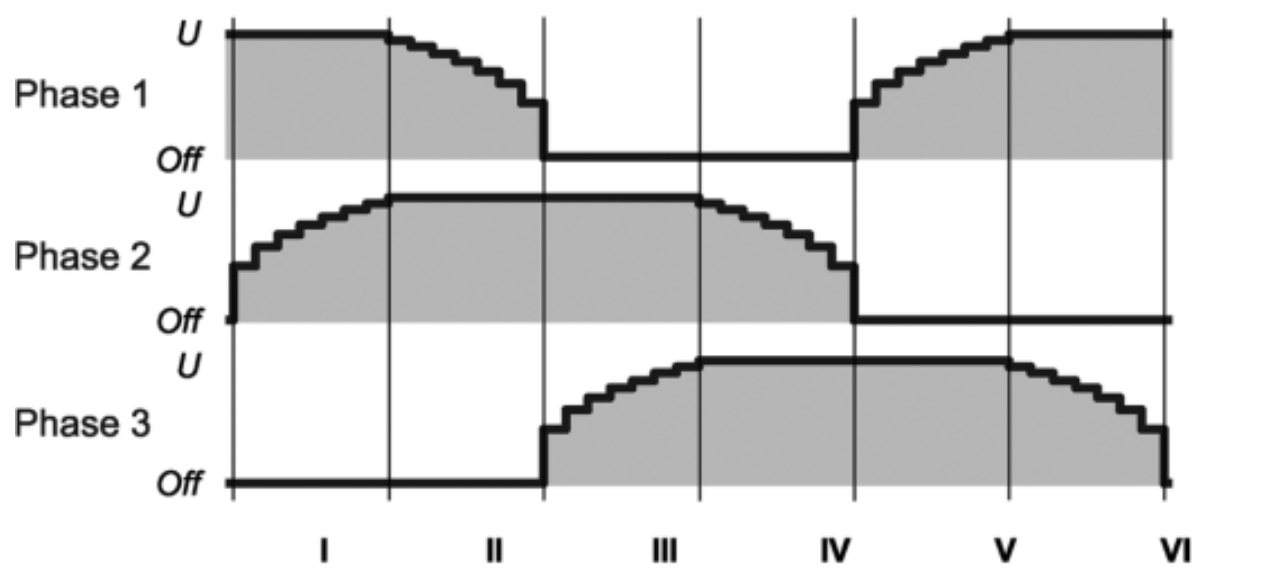
图 8.微步进电压序列,以得到更平稳的步进过程。
在考虑驱动模式的同时,我们需要注意到转子的刚度影响不仅仅在于抵抗静电力的驱动:当静电驱动扭矩将转子从一个稳定的位置向外移动到另一个位置时,挠性体的机械刚度会抵消其运动并使转子减速。然而,当转子向其静止位置移动时,机械恢复力在同一方向上发挥作用,进一步加速转子,使其更容易跳步。所以在恢复的情况下,机械恢复力可用于在两个位置之间移动转子,而驱动扭矩将用于减速转子的运动,这将使电机的运行更加稳定。
最后,因为时间原因,本文没有进行三维有限元建模分析的工作。通过有限元模型,我们或许可以估计出运行过程中的旋转中心偏移,枢轴更准确的转动刚度和转子的转动惯量。
Conclusion
本文介绍了一种采用“蝴蝶形”挠性悬挂枢轴的三相静电 MEMS 旋转电机的设计、建模和制备工艺。该电机具有精确、可重复和可靠的双向步进运动,可用于驱动微泵、微阀或微型镜片等设备。通过数学建模,我们证明了该电机在 50V 驱动电压下最大能输出 12.5mNm 的扭矩,满足了 2mNm 以上输出力矩和 50V 以下驱动电压的要求。此外,我们还分析了该电机结构设计中的参数和驱动电压对性能影响的规律,并提出了优化方案。总之,本文基于静电 MEMS 旋转电机领域给出了一些基础的研究方法与思路,具有一定的理论和应用价值。
Acknowledgment
本文的动力来源于《微系统设计与系统集成技术》课程大作业。本文的结构设计主要参考自文献[4]和文献[6],关于挠性枢轴的旋转刚度建模主要参考自文献[4]。制备工艺主要参考自文献[3]和文献[7]。
Citations
[1] C. Livermore, A. R. Forte, T. Lyszczarz, S. D. Umans, A. A. Ayon and J. H. Lang, “A high-power MEMS electric induction motor,” in Journal of Microelectromechanical Systems, vol. 13, no. 3, pp. 465-471, June 2004
[2] M. Takato, Y. Yokozeki, K. Mishima, Y. Han, K. Saito and F. Uchikoba, “Design of electromagnetic induction type MEMS motor with multilayer ceramic three-dimensional coil,” 2016 International Conference on Electronics Packaging (ICEP), Hokkaido, Japan, 2016
[3] S. Merzaghi, C. Koechli and Y. Perriard, “Development of a Hybrid MEMS BLDC Micromotor,” in IEEE Transactions on Industry Applications, vol. 47, no. 1, pp. 3-11, Jan.-Feb. 2011
[4]E. Sarajlic, C. Yamahata, M. Cordero and H. Fujita, “Three-Phase Electrostatic Rotary Stepper Micromotor With a Flexural Pivot Bearing,” in Journal of Microelectromechanical Systems, vol. 19, no. 2, pp. 338-349, April 2010
[5] A. S. Algamili, M. H. M. Khir, J. O. Dennis and N. A. M. Amin, “A Review of Actuation and Sensing Mechanisms in MEMS-Based Sensor Devices,” Nanoscale Research Letters, vol. 16, no. 1, pp. 1-16, Jan. 2021.
[6] S. Henein, P. Spanoudakis, S. Droz, L. I. Myklebust and E. Onillon, “Flexure pivot for aerospace mechanisms”, Proc. 10th ESMATSESA SP, pp. 285-288, 2003.
[7] E. Sarajlic, C. Yamahata, M. Cordero and H. Fujita, “An electrostatic 3-phase linear stepper motor fabricated by vertical trench isolation technology”, J. Micromech. Microeng., vol. 19, no. 7, pp. 074001-1-074001-7, Jul. 2009.
[8] W. Gao, S. Sattayasamitsathit and J. Wang, “Fabrication of Micro/Nanoscale Motors,” Chemical Reviews, vol. 115, no. 16, pp. 8704-8735, Aug. 2015.